Generate (population-average) relative treatment effects. If a ML-NMR or meta-regression model was fitted, these are specific to each study population.
Usage
relative_effects(
x,
newdata = NULL,
study = NULL,
all_contrasts = FALSE,
trt_ref = NULL,
probs = c(0.025, 0.25, 0.5, 0.75, 0.975),
predictive_distribution = FALSE,
summary = TRUE
)Arguments
- x
A
stan_nmaobject created bynma()- newdata
Only used if a regression model is fitted. A data frame of study details, one row per study, giving the covariate values at which to produce relative effects. Column names must match variables in the regression model. If
NULL, relative effects are produced for all studies in the network.- study
Column of
newdatawhich specifies study names, otherwise studies will be labelled by row number.- all_contrasts
Logical, generate estimates for all contrasts (
TRUE), or just the "basic" contrasts against the network reference treatment (FALSE)? DefaultFALSE.- trt_ref
Reference treatment to construct relative effects against, if
all_contrasts = FALSE. By default, relative effects will be against the network reference treatment. Coerced to character string.- probs
Numeric vector of quantiles of interest to present in computed summary, default
c(0.025, 0.25, 0.5, 0.75, 0.975)- predictive_distribution
Logical, when a random effects model has been fitted, should the predictive distribution for relative effects in a new study be returned? Default
FALSE.- summary
Logical, calculate posterior summaries? Default
TRUE.
Value
A nma_summary object if summary = TRUE, otherwise a list
containing a 3D MCMC array of samples and (for regression models) a data
frame of study information.
See also
plot.nma_summary() for plotting the relative effects.
Examples
## Smoking cessation
# \donttest{
# Run smoking RE NMA example if not already available
if (!exists("smk_fit_RE")) example("example_smk_re", run.donttest = TRUE)
# }
# \donttest{
# Produce relative effects
smk_releff_RE <- relative_effects(smk_fit_RE)
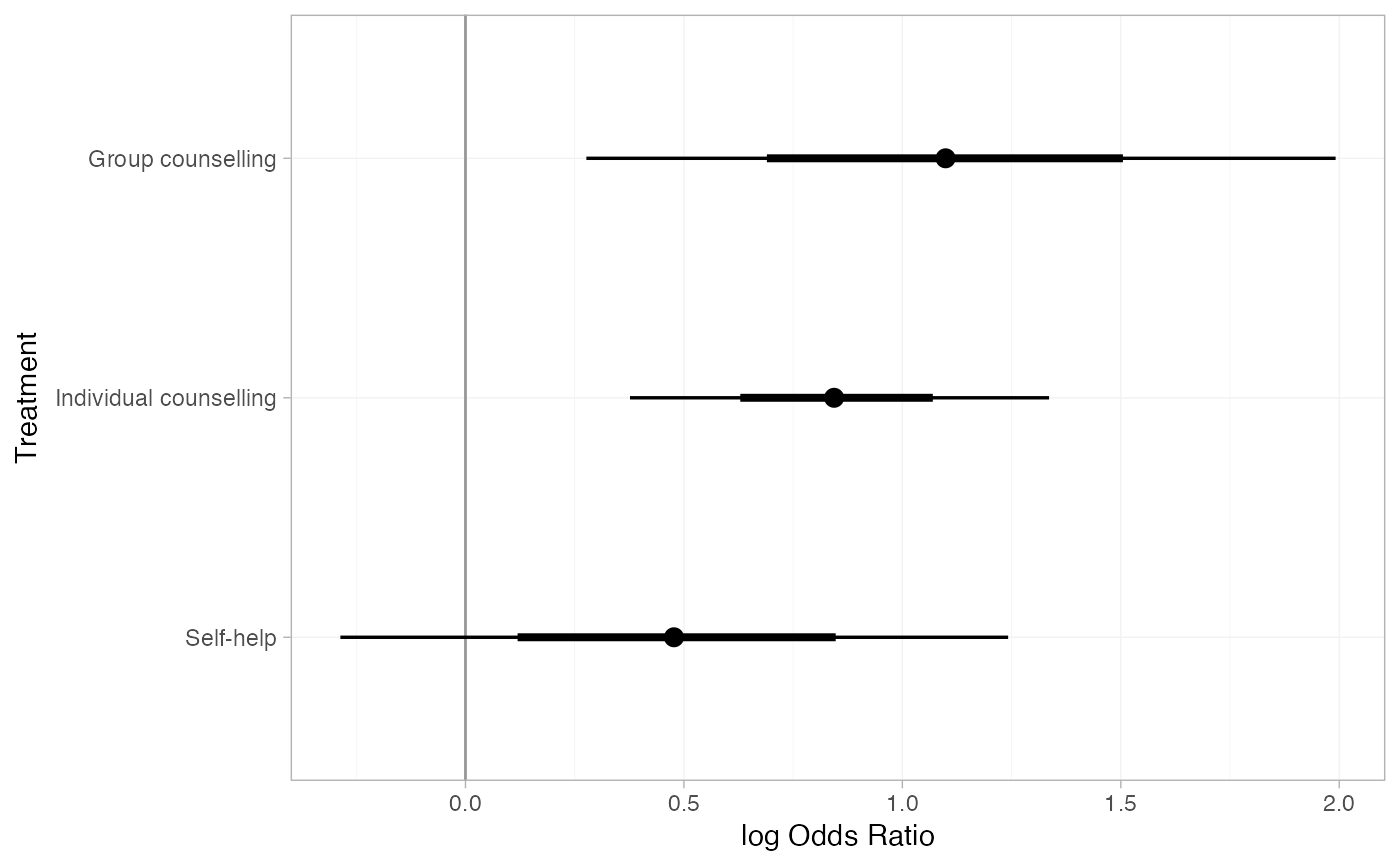
smk_releff_RE
#> mean sd 2.5% 25% 50% 75% 97.5% Bulk_ESS
#> d[Group counselling] 1.11 0.45 0.26 0.82 1.10 1.39 2.05 1541
#> d[Individual counselling] 0.85 0.24 0.39 0.69 0.84 1.01 1.36 985
#> d[Self-help] 0.48 0.41 -0.30 0.22 0.48 0.74 1.32 1483
#> Tail_ESS Rhat
#> d[Group counselling] 2173 1
#> d[Individual counselling] 1773 1
#> d[Self-help] 1676 1
plot(smk_releff_RE, ref_line = 0)
 # Relative effects for all pairwise comparisons
relative_effects(smk_fit_RE, all_contrasts = TRUE)
#> mean sd 2.5% 25% 50%
#> d[Group counselling vs. No intervention] 1.11 0.45 0.26 0.82 1.10
#> d[Individual counselling vs. No intervention] 0.85 0.24 0.39 0.69 0.84
#> d[Self-help vs. No intervention] 0.48 0.41 -0.30 0.22 0.48
#> d[Individual counselling vs. Group counselling] -0.26 0.42 -1.10 -0.53 -0.25
#> d[Self-help vs. Group counselling] -0.62 0.49 -1.66 -0.94 -0.62
#> d[Self-help vs. Individual counselling] -0.37 0.42 -1.19 -0.64 -0.36
#> 75% 97.5% Bulk_ESS Tail_ESS
#> d[Group counselling vs. No intervention] 1.39 2.05 1541 2173
#> d[Individual counselling vs. No intervention] 1.01 1.36 985 1773
#> d[Self-help vs. No intervention] 0.74 1.32 1483 1676
#> d[Individual counselling vs. Group counselling] 0.02 0.56 2431 2536
#> d[Self-help vs. Group counselling] -0.30 0.33 2629 2708
#> d[Self-help vs. Individual counselling] -0.10 0.44 2025 2188
#> Rhat
#> d[Group counselling vs. No intervention] 1
#> d[Individual counselling vs. No intervention] 1
#> d[Self-help vs. No intervention] 1
#> d[Individual counselling vs. Group counselling] 1
#> d[Self-help vs. Group counselling] 1
#> d[Self-help vs. Individual counselling] 1
# Relative effects against a different reference treatment
relative_effects(smk_fit_RE, trt_ref = "Self-help")
#> mean sd 2.5% 25% 50% 75% 97.5% Bulk_ESS
#> d[No intervention] -0.48 0.41 -1.32 -0.74 -0.48 -0.22 0.30 1483
#> d[Group counselling] 0.62 0.49 -0.33 0.30 0.62 0.94 1.66 2629
#> d[Individual counselling] 0.37 0.42 -0.44 0.10 0.36 0.64 1.19 2025
#> Tail_ESS Rhat
#> d[No intervention] 1676 1
#> d[Group counselling] 2708 1
#> d[Individual counselling] 2188 1
# Transforming to odds ratios
# We work with the array of relative effects samples
LOR_array <- as.array(smk_releff_RE)
OR_array <- exp(LOR_array)
# mcmc_array objects can be summarised to produce a nma_summary object
smk_OR_RE <- summary(OR_array)
# This can then be printed or plotted
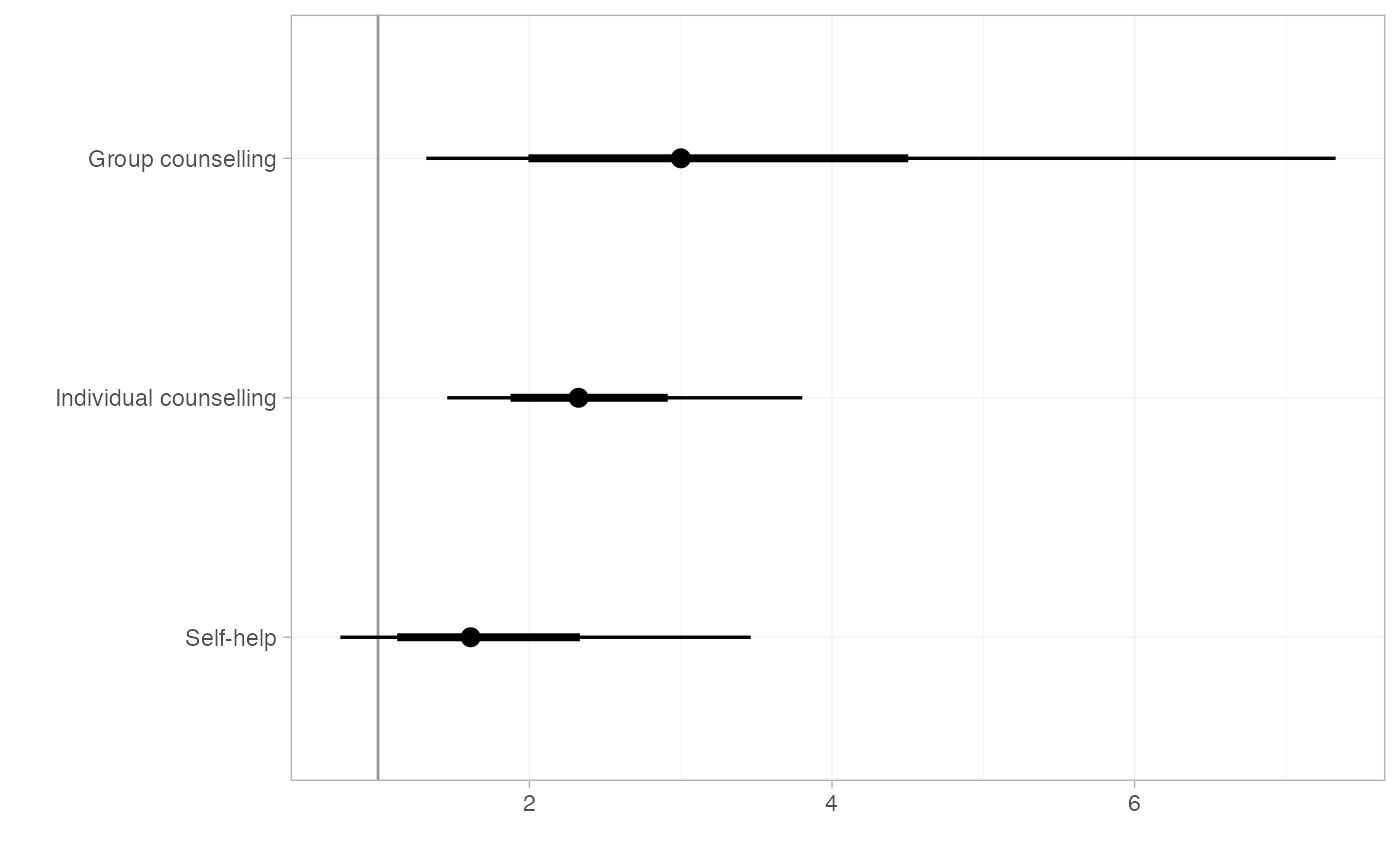
smk_OR_RE
#> mean sd 2.5% 25% 50% 75% 97.5% Bulk_ESS Tail_ESS
#> d[Group counselling] 3.36 1.71 1.29 2.28 3.01 4.02 7.79 1541 2173
#> d[Individual counselling] 2.42 0.62 1.48 1.98 2.32 2.74 3.91 985 1773
#> d[Self-help] 1.77 0.80 0.74 1.25 1.62 2.10 3.74 1483 1676
#> Rhat
#> d[Group counselling] 1
#> d[Individual counselling] 1
#> d[Self-help] 1
plot(smk_OR_RE, ref_line = 1)
# Relative effects for all pairwise comparisons
relative_effects(smk_fit_RE, all_contrasts = TRUE)
#> mean sd 2.5% 25% 50%
#> d[Group counselling vs. No intervention] 1.11 0.45 0.26 0.82 1.10
#> d[Individual counselling vs. No intervention] 0.85 0.24 0.39 0.69 0.84
#> d[Self-help vs. No intervention] 0.48 0.41 -0.30 0.22 0.48
#> d[Individual counselling vs. Group counselling] -0.26 0.42 -1.10 -0.53 -0.25
#> d[Self-help vs. Group counselling] -0.62 0.49 -1.66 -0.94 -0.62
#> d[Self-help vs. Individual counselling] -0.37 0.42 -1.19 -0.64 -0.36
#> 75% 97.5% Bulk_ESS Tail_ESS
#> d[Group counselling vs. No intervention] 1.39 2.05 1541 2173
#> d[Individual counselling vs. No intervention] 1.01 1.36 985 1773
#> d[Self-help vs. No intervention] 0.74 1.32 1483 1676
#> d[Individual counselling vs. Group counselling] 0.02 0.56 2431 2536
#> d[Self-help vs. Group counselling] -0.30 0.33 2629 2708
#> d[Self-help vs. Individual counselling] -0.10 0.44 2025 2188
#> Rhat
#> d[Group counselling vs. No intervention] 1
#> d[Individual counselling vs. No intervention] 1
#> d[Self-help vs. No intervention] 1
#> d[Individual counselling vs. Group counselling] 1
#> d[Self-help vs. Group counselling] 1
#> d[Self-help vs. Individual counselling] 1
# Relative effects against a different reference treatment
relative_effects(smk_fit_RE, trt_ref = "Self-help")
#> mean sd 2.5% 25% 50% 75% 97.5% Bulk_ESS
#> d[No intervention] -0.48 0.41 -1.32 -0.74 -0.48 -0.22 0.30 1483
#> d[Group counselling] 0.62 0.49 -0.33 0.30 0.62 0.94 1.66 2629
#> d[Individual counselling] 0.37 0.42 -0.44 0.10 0.36 0.64 1.19 2025
#> Tail_ESS Rhat
#> d[No intervention] 1676 1
#> d[Group counselling] 2708 1
#> d[Individual counselling] 2188 1
# Transforming to odds ratios
# We work with the array of relative effects samples
LOR_array <- as.array(smk_releff_RE)
OR_array <- exp(LOR_array)
# mcmc_array objects can be summarised to produce a nma_summary object
smk_OR_RE <- summary(OR_array)
# This can then be printed or plotted
smk_OR_RE
#> mean sd 2.5% 25% 50% 75% 97.5% Bulk_ESS Tail_ESS
#> d[Group counselling] 3.36 1.71 1.29 2.28 3.01 4.02 7.79 1541 2173
#> d[Individual counselling] 2.42 0.62 1.48 1.98 2.32 2.74 3.91 985 1773
#> d[Self-help] 1.77 0.80 0.74 1.25 1.62 2.10 3.74 1483 1676
#> Rhat
#> d[Group counselling] 1
#> d[Individual counselling] 1
#> d[Self-help] 1
plot(smk_OR_RE, ref_line = 1)
 # }
## Plaque psoriasis ML-NMR
# \donttest{
# Run plaque psoriasis ML-NMR example if not already available
if (!exists("pso_fit")) example("example_pso_mlnmr", run.donttest = TRUE)
# }
# \donttest{
# Produce population-adjusted relative effects for all study populations in
# the network
pso_releff <- relative_effects(pso_fit)
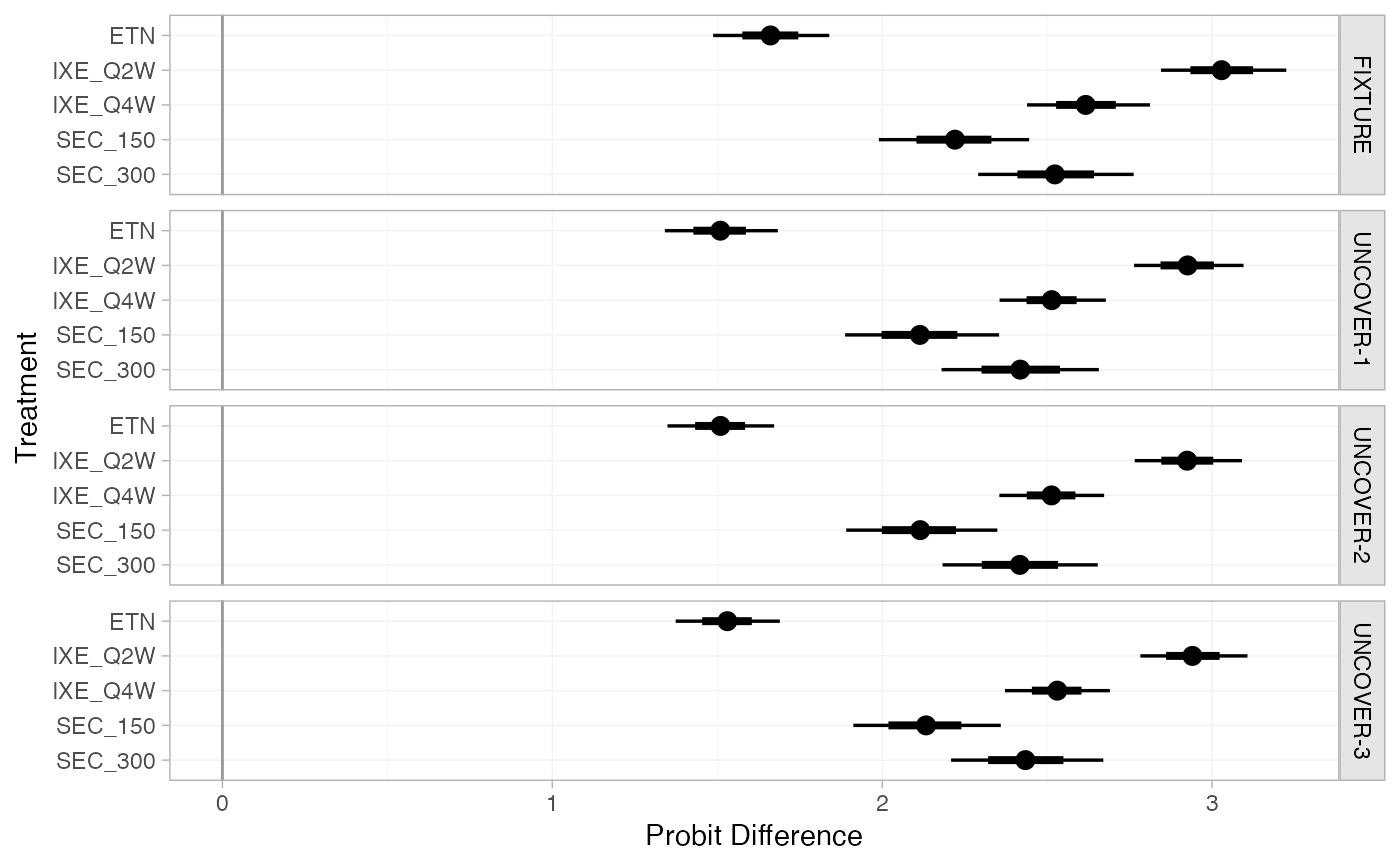
pso_releff
#> ---------------------------------------------------------------- Study: FIXTURE ----
#>
#> Covariate values:
#> durnpso prevsys bsa weight psa
#> 1.6 0.62 0.34 8.34 0.14
#>
#> mean sd 2.5% 25% 50% 75% 97.5% Bulk_ESS Tail_ESS Rhat
#> d[FIXTURE: ETN] 1.66 0.09 1.48 1.60 1.66 1.72 1.85 4491 3470 1
#> d[FIXTURE: IXE_Q2W] 3.03 0.10 2.83 2.96 3.03 3.10 3.23 5316 3002 1
#> d[FIXTURE: IXE_Q4W] 2.61 0.09 2.43 2.55 2.62 2.67 2.81 5697 3344 1
#> d[FIXTURE: SEC_150] 2.22 0.12 1.99 2.14 2.22 2.30 2.45 4841 3458 1
#> d[FIXTURE: SEC_300] 2.52 0.13 2.28 2.44 2.52 2.61 2.77 5571 3209 1
#>
#> -------------------------------------------------------------- Study: UNCOVER-1 ----
#>
#> Covariate values:
#> durnpso prevsys bsa weight psa
#> 2 0.73 0.28 9.24 0.28
#>
#> mean sd 2.5% 25% 50% 75% 97.5% Bulk_ESS Tail_ESS
#> d[UNCOVER-1: ETN] 1.51 0.09 1.35 1.45 1.51 1.56 1.68 4528 3451
#> d[UNCOVER-1: IXE_Q2W] 2.92 0.09 2.75 2.86 2.92 2.99 3.10 5090 2955
#> d[UNCOVER-1: IXE_Q4W] 2.51 0.08 2.35 2.45 2.51 2.56 2.68 5478 3206
#> d[UNCOVER-1: SEC_150] 2.11 0.12 1.89 2.03 2.11 2.19 2.35 5096 3659
#> d[UNCOVER-1: SEC_300] 2.42 0.13 2.16 2.33 2.42 2.50 2.67 5974 3325
#> Rhat
#> d[UNCOVER-1: ETN] 1
#> d[UNCOVER-1: IXE_Q2W] 1
#> d[UNCOVER-1: IXE_Q4W] 1
#> d[UNCOVER-1: SEC_150] 1
#> d[UNCOVER-1: SEC_300] 1
#>
#> -------------------------------------------------------------- Study: UNCOVER-2 ----
#>
#> Covariate values:
#> durnpso prevsys bsa weight psa
#> 1.87 0.64 0.27 9.17 0.24
#>
#> mean sd 2.5% 25% 50% 75% 97.5% Bulk_ESS Tail_ESS
#> d[UNCOVER-2: ETN] 1.51 0.08 1.35 1.45 1.51 1.56 1.67 4689 3363
#> d[UNCOVER-2: IXE_Q2W] 2.92 0.09 2.75 2.86 2.92 2.98 3.10 5222 2920
#> d[UNCOVER-2: IXE_Q4W] 2.51 0.08 2.35 2.46 2.51 2.56 2.67 5572 3356
#> d[UNCOVER-2: SEC_150] 2.11 0.12 1.89 2.03 2.11 2.19 2.35 5146 3446
#> d[UNCOVER-2: SEC_300] 2.42 0.13 2.17 2.33 2.42 2.50 2.67 6058 3302
#> Rhat
#> d[UNCOVER-2: ETN] 1
#> d[UNCOVER-2: IXE_Q2W] 1
#> d[UNCOVER-2: IXE_Q4W] 1
#> d[UNCOVER-2: SEC_150] 1
#> d[UNCOVER-2: SEC_300] 1
#>
#> -------------------------------------------------------------- Study: UNCOVER-3 ----
#>
#> Covariate values:
#> durnpso prevsys bsa weight psa
#> 1.78 0.59 0.28 9.01 0.2
#>
#> mean sd 2.5% 25% 50% 75% 97.5% Bulk_ESS Tail_ESS
#> d[UNCOVER-3: ETN] 1.53 0.08 1.37 1.47 1.53 1.58 1.69 4649 3480
#> d[UNCOVER-3: IXE_Q2W] 2.94 0.09 2.76 2.88 2.94 3.00 3.12 5265 3056
#> d[UNCOVER-3: IXE_Q4W] 2.53 0.08 2.37 2.47 2.53 2.58 2.69 5667 3343
#> d[UNCOVER-3: SEC_150] 2.13 0.12 1.91 2.05 2.13 2.21 2.36 5128 3496
#> d[UNCOVER-3: SEC_300] 2.43 0.12 2.19 2.35 2.43 2.52 2.68 6009 3531
#> Rhat
#> d[UNCOVER-3: ETN] 1
#> d[UNCOVER-3: IXE_Q2W] 1
#> d[UNCOVER-3: IXE_Q4W] 1
#> d[UNCOVER-3: SEC_150] 1
#> d[UNCOVER-3: SEC_300] 1
#>
plot(pso_releff, ref_line = 0)
# }
## Plaque psoriasis ML-NMR
# \donttest{
# Run plaque psoriasis ML-NMR example if not already available
if (!exists("pso_fit")) example("example_pso_mlnmr", run.donttest = TRUE)
# }
# \donttest{
# Produce population-adjusted relative effects for all study populations in
# the network
pso_releff <- relative_effects(pso_fit)
pso_releff
#> ---------------------------------------------------------------- Study: FIXTURE ----
#>
#> Covariate values:
#> durnpso prevsys bsa weight psa
#> 1.6 0.62 0.34 8.34 0.14
#>
#> mean sd 2.5% 25% 50% 75% 97.5% Bulk_ESS Tail_ESS Rhat
#> d[FIXTURE: ETN] 1.66 0.09 1.48 1.60 1.66 1.72 1.85 4491 3470 1
#> d[FIXTURE: IXE_Q2W] 3.03 0.10 2.83 2.96 3.03 3.10 3.23 5316 3002 1
#> d[FIXTURE: IXE_Q4W] 2.61 0.09 2.43 2.55 2.62 2.67 2.81 5697 3344 1
#> d[FIXTURE: SEC_150] 2.22 0.12 1.99 2.14 2.22 2.30 2.45 4841 3458 1
#> d[FIXTURE: SEC_300] 2.52 0.13 2.28 2.44 2.52 2.61 2.77 5571 3209 1
#>
#> -------------------------------------------------------------- Study: UNCOVER-1 ----
#>
#> Covariate values:
#> durnpso prevsys bsa weight psa
#> 2 0.73 0.28 9.24 0.28
#>
#> mean sd 2.5% 25% 50% 75% 97.5% Bulk_ESS Tail_ESS
#> d[UNCOVER-1: ETN] 1.51 0.09 1.35 1.45 1.51 1.56 1.68 4528 3451
#> d[UNCOVER-1: IXE_Q2W] 2.92 0.09 2.75 2.86 2.92 2.99 3.10 5090 2955
#> d[UNCOVER-1: IXE_Q4W] 2.51 0.08 2.35 2.45 2.51 2.56 2.68 5478 3206
#> d[UNCOVER-1: SEC_150] 2.11 0.12 1.89 2.03 2.11 2.19 2.35 5096 3659
#> d[UNCOVER-1: SEC_300] 2.42 0.13 2.16 2.33 2.42 2.50 2.67 5974 3325
#> Rhat
#> d[UNCOVER-1: ETN] 1
#> d[UNCOVER-1: IXE_Q2W] 1
#> d[UNCOVER-1: IXE_Q4W] 1
#> d[UNCOVER-1: SEC_150] 1
#> d[UNCOVER-1: SEC_300] 1
#>
#> -------------------------------------------------------------- Study: UNCOVER-2 ----
#>
#> Covariate values:
#> durnpso prevsys bsa weight psa
#> 1.87 0.64 0.27 9.17 0.24
#>
#> mean sd 2.5% 25% 50% 75% 97.5% Bulk_ESS Tail_ESS
#> d[UNCOVER-2: ETN] 1.51 0.08 1.35 1.45 1.51 1.56 1.67 4689 3363
#> d[UNCOVER-2: IXE_Q2W] 2.92 0.09 2.75 2.86 2.92 2.98 3.10 5222 2920
#> d[UNCOVER-2: IXE_Q4W] 2.51 0.08 2.35 2.46 2.51 2.56 2.67 5572 3356
#> d[UNCOVER-2: SEC_150] 2.11 0.12 1.89 2.03 2.11 2.19 2.35 5146 3446
#> d[UNCOVER-2: SEC_300] 2.42 0.13 2.17 2.33 2.42 2.50 2.67 6058 3302
#> Rhat
#> d[UNCOVER-2: ETN] 1
#> d[UNCOVER-2: IXE_Q2W] 1
#> d[UNCOVER-2: IXE_Q4W] 1
#> d[UNCOVER-2: SEC_150] 1
#> d[UNCOVER-2: SEC_300] 1
#>
#> -------------------------------------------------------------- Study: UNCOVER-3 ----
#>
#> Covariate values:
#> durnpso prevsys bsa weight psa
#> 1.78 0.59 0.28 9.01 0.2
#>
#> mean sd 2.5% 25% 50% 75% 97.5% Bulk_ESS Tail_ESS
#> d[UNCOVER-3: ETN] 1.53 0.08 1.37 1.47 1.53 1.58 1.69 4649 3480
#> d[UNCOVER-3: IXE_Q2W] 2.94 0.09 2.76 2.88 2.94 3.00 3.12 5265 3056
#> d[UNCOVER-3: IXE_Q4W] 2.53 0.08 2.37 2.47 2.53 2.58 2.69 5667 3343
#> d[UNCOVER-3: SEC_150] 2.13 0.12 1.91 2.05 2.13 2.21 2.36 5128 3496
#> d[UNCOVER-3: SEC_300] 2.43 0.12 2.19 2.35 2.43 2.52 2.68 6009 3531
#> Rhat
#> d[UNCOVER-3: ETN] 1
#> d[UNCOVER-3: IXE_Q2W] 1
#> d[UNCOVER-3: IXE_Q4W] 1
#> d[UNCOVER-3: SEC_150] 1
#> d[UNCOVER-3: SEC_300] 1
#>
plot(pso_releff, ref_line = 0)
 # Produce population-adjusted relative effects for a different target
# population
new_agd_means <- data.frame(
bsa = 0.6,
prevsys = 0.1,
psa = 0.2,
weight = 10,
durnpso = 3)
relative_effects(pso_fit, newdata = new_agd_means)
#> ------------------------------------------------------------------ Study: New 1 ----
#>
#> Covariate values:
#> durnpso prevsys bsa weight psa
#> 3 0.1 0.6 10 0.2
#>
#> mean sd 2.5% 25% 50% 75% 97.5% Bulk_ESS Tail_ESS Rhat
#> d[New 1: ETN] 1.25 0.23 0.79 1.09 1.25 1.41 1.71 6583 3193 1
#> d[New 1: IXE_Q2W] 2.88 0.22 2.45 2.73 2.88 3.03 3.33 7024 2927 1
#> d[New 1: IXE_Q4W] 2.47 0.22 2.05 2.33 2.47 2.62 2.91 7604 3060 1
#> d[New 1: SEC_150] 2.07 0.23 1.63 1.93 2.07 2.22 2.51 6626 2952 1
#> d[New 1: SEC_300] 2.38 0.23 1.93 2.22 2.38 2.53 2.83 6772 3129 1
#>
# }
# Produce population-adjusted relative effects for a different target
# population
new_agd_means <- data.frame(
bsa = 0.6,
prevsys = 0.1,
psa = 0.2,
weight = 10,
durnpso = 3)
relative_effects(pso_fit, newdata = new_agd_means)
#> ------------------------------------------------------------------ Study: New 1 ----
#>
#> Covariate values:
#> durnpso prevsys bsa weight psa
#> 3 0.1 0.6 10 0.2
#>
#> mean sd 2.5% 25% 50% 75% 97.5% Bulk_ESS Tail_ESS Rhat
#> d[New 1: ETN] 1.25 0.23 0.79 1.09 1.25 1.41 1.71 6583 3193 1
#> d[New 1: IXE_Q2W] 2.88 0.22 2.45 2.73 2.88 3.03 3.33 7024 2927 1
#> d[New 1: IXE_Q4W] 2.47 0.22 2.05 2.33 2.47 2.62 2.91 7604 3060 1
#> d[New 1: SEC_150] 2.07 0.23 1.63 1.93 2.07 2.22 2.51 6626 2952 1
#> d[New 1: SEC_300] 2.38 0.23 1.93 2.22 2.38 2.53 2.83 6772 3129 1
#>
# }