Example: Dietary fat

library(multinma)
options(mc.cores = parallel::detectCores())

#> For execution on a local, multicore CPU with excess RAM we recommend calling
#> options(mc.cores = parallel::detectCores())
#> 
#> Attaching package: 'multinma'
#> The following objects are masked from 'package:stats':
#> 
#>     dgamma, pgamma, qgamma

This vignette describes the analysis of 10 trials comparing reduced fat diets to control (non-reduced fat diets) for preventing mortality (Hooper et al. 2000; Dias et al. 2011). The data are available in this package as dietary_fat:

head(dietary_fat)
#>   studyn            studyc trtn        trtc   r    n      E
#> 1      1              DART    1     Control 113 1015 1917.0
#> 2      1              DART    2 Reduced Fat 111 1018 1925.0
#> 3      2 London Corn/Olive    1     Control   1   26   43.6
#> 4      2 London Corn/Olive    2 Reduced Fat   5   28   41.3
#> 5      2 London Corn/Olive    2 Reduced Fat   3   26   38.0
#> 6      3    London Low Fat    1     Control  24  129  393.5

Setting up the network

We begin by setting up the network - here just a pairwise meta-analysis. We have arm-level rate data giving the number of deaths (r) and the person-years at risk (E) in each arm, so we use the function set_agd_arm(). We set “Control” as the reference treatment.

diet_net <- set_agd_arm(dietary_fat, 
                        study = studyc,
                        trt = trtc,
                        r = r, 
                        E = E,
                        trt_ref = "Control",
                        sample_size = n)
diet_net
#> A network with 10 AgD studies (arm-based).
#> 
#> ------------------------------------------------------- AgD studies (arm-based) ---- 
#>  Study                   Treatment arms                        
#>  DART                    2: Control | Reduced Fat              
#>  London Corn/Olive       3: Control | Reduced Fat | Reduced Fat
#>  London Low Fat          2: Control | Reduced Fat              
#>  Minnesota Coronary      2: Control | Reduced Fat              
#>  MRC Soya                2: Control | Reduced Fat              
#>  Oslo Diet-Heart         2: Control | Reduced Fat              
#>  STARS                   2: Control | Reduced Fat              
#>  Sydney Diet-Heart       2: Control | Reduced Fat              
#>  Veterans Administration 2: Control | Reduced Fat              
#>  Veterans Diet & Skin CA 2: Control | Reduced Fat              
#> 
#>  Outcome type: rate
#> ------------------------------------------------------------------------------------
#> Total number of treatments: 2
#> Total number of studies: 10
#> Reference treatment is: Control
#> Network is connected

We also specify the optional sample_size argument, although it is not strictly necessary here. In this case sample_size would only be required to produce a network plot with nodes weighted by sample size, and a network plot is not particularly informative for a meta-analysis of only two treatments. (The sample_size argument is more important when a regression model is specified, since it also enables automatic centering of predictors and production of predictions for studies in the network, see ?set_agd_arm.)

Meta-analysis models

We fit both fixed effect (FE) and random effects (RE) models.

Fixed effect meta-analysis

First, we fit a fixed effect model using the nma() function with trt_effects = "fixed". We use $\mathrm{N}(0, 100^2)$ prior distributions for the treatment effects $d_k$ and study-specific intercepts $\mu_j$. We can examine the range of parameter values implied by these prior distributions with the summary() method:

summary(normal(scale = 100))
#> A Normal prior distribution: location = 0, scale = 100.
#> 50% of the prior density lies between -67.45 and 67.45.
#> 95% of the prior density lies between -196 and 196.

The model is fitted using the nma() function. By default, this will use a Poisson likelihood with a log link function, auto-detected from the data.

diet_fit_FE <- nma(diet_net, 
                   trt_effects = "fixed",
                   prior_intercept = normal(scale = 100),
                   prior_trt = normal(scale = 100))
#> 00 [ 20%]  (Warmup)
#> Chain 2: Iteration:  400 / 2000 [ 20%]  (Warmup)
#> Chain 1: Iteration:  400 / 2000 [ 20%]  (Warmup)
#> Chain 3: Iteration:  600 / 2000 [ 30%]  (Warmup)
#> Chain 1: Iteration:  600 / 2000 [ 30%]  (Warmup)
#> Chain 2: Iteration:  600 / 2000 [ 30%]  (Warmup)
#> Chain 3: Iteration:  800 / 2000 [ 40%]  (Warmup)
#> Chain 1: Iteration:  800 / 2000 [ 40%]  (Warmup)
#> Chain 2: Iteration:  800 / 2000 [ 40%]  (Warmup)
#> Chain 3: Iteration: 1000 / 2000 [ 50%]  (Warmup)
#> Chain 3: Iteration: 1001 / 2000 [ 50%]  (Sampling)
#> Chain 1: Iteration: 1000 / 2000 [ 50%]  (Warmup)
#> Chain 1: Iteration: 1001 / 2000 [ 50%]  (Sampling)
#> Chain 2: Iteration: 1000 / 2000 [ 50%]  (Warmup)
#> Chain 2: Iteration: 1001 / 2000 [ 50%]  (Sampling)
#> Chain 3: Iteration: 1200 / 2000 [ 60%]  (Sampling)
#> Chain 1: Iteration: 1200 / 2000 [ 60%]  (Sampling)
#> Chain 2: Iteration: 1200 / 2000 [ 60%]  (Sampling)
#> Chain 3: Iteration: 1400 / 2000 [ 70%]  (Sampling)
#> Chain 1: Iteration: 1400 / 2000 [ 70%]  (Sampling)
#> Chain 2: Iteration: 1400 / 2000 [ 70%]  (Sampling)
#> Chain 3: Iteration: 1600 / 2000 [ 80%]  (Sampling)
#> Chain 1: Iteration: 1600 / 2000 [ 80%]  (Sampling)
#> Chain 2: Iteration: 1600 / 2000 [ 80%]  (Sampling)
#> Chain 3: Iteration: 1800 / 2000 [ 90%]  (Sampling)
#> Chain 1: Iteration: 1800 / 2000 [ 90%]  (Sampling)
#> Chain 2: Iteration: 1800 / 2000 [ 90%]  (Sampling)
#> Chain 3: Iteration: 2000 / 2000 [100%]  (Sampling)
#> Chain 3: 
#> Chain 3:  Elapsed Time: 0.043 seconds (Warm-up)
#> Chain 3:                0.029 seconds (Sampling)
#> Chain 3:                0.072 seconds (Total)
#> Chain 3: 
#> Chain 1: Iteration: 2000 / 2000 [100%]  (Sampling)
#> Chain 1: 
#> Chain 1:  Elapsed Time: 0.044 seconds (Warm-up)
#> Chain 1:                0.03 seconds (Sampling)
#> Chain 1:                0.074 seconds (Total)
#> Chain 1: 
#> Chain 2: Iteration: 2000 / 2000 [100%]  (Sampling)
#> Chain 2: 
#> Chain 2:  Elapsed Time: 0.045 seconds (Warm-up)
#> Chain 2:                0.032 seconds (Sampling)
#> Chain 2:                0.077 seconds (Total)
#> Chain 2:

Basic parameter summaries are given by the print() method:

diet_fit_FE
#> A fixed effects NMA with a poisson likelihood (log link).
#> Inference for Stan model: poisson.
#> 4 chains, each with iter=2000; warmup=1000; thin=1; 
#> post-warmup draws per chain=1000, total post-warmup draws=4000.
#> 
#>                   mean se_mean   sd    2.5%     25%     50%     75%   97.5% n_eff Rhat
#> d[Reduced Fat]   -0.01    0.00 0.05   -0.11   -0.04   -0.01    0.03    0.10  3568    1
#> lp__           5386.16    0.06 2.49 5380.38 5384.77 5386.50 5387.97 5389.91  1586    1
#> 
#> Samples were drawn using NUTS(diag_e) at Tue Sep 24 09:06:20 2024.
#> For each parameter, n_eff is a crude measure of effective sample size,
#> and Rhat is the potential scale reduction factor on split chains (at 
#> convergence, Rhat=1).

By default, summaries of the study-specific intercepts $\mu_j$ are hidden, but could be examined by changing the pars argument:

# Not run
print(diet_fit_FE, pars = c("d", "mu"))

The prior and posterior distributions can be compared visually using the plot_prior_posterior() function:

plot_prior_posterior(diet_fit_FE)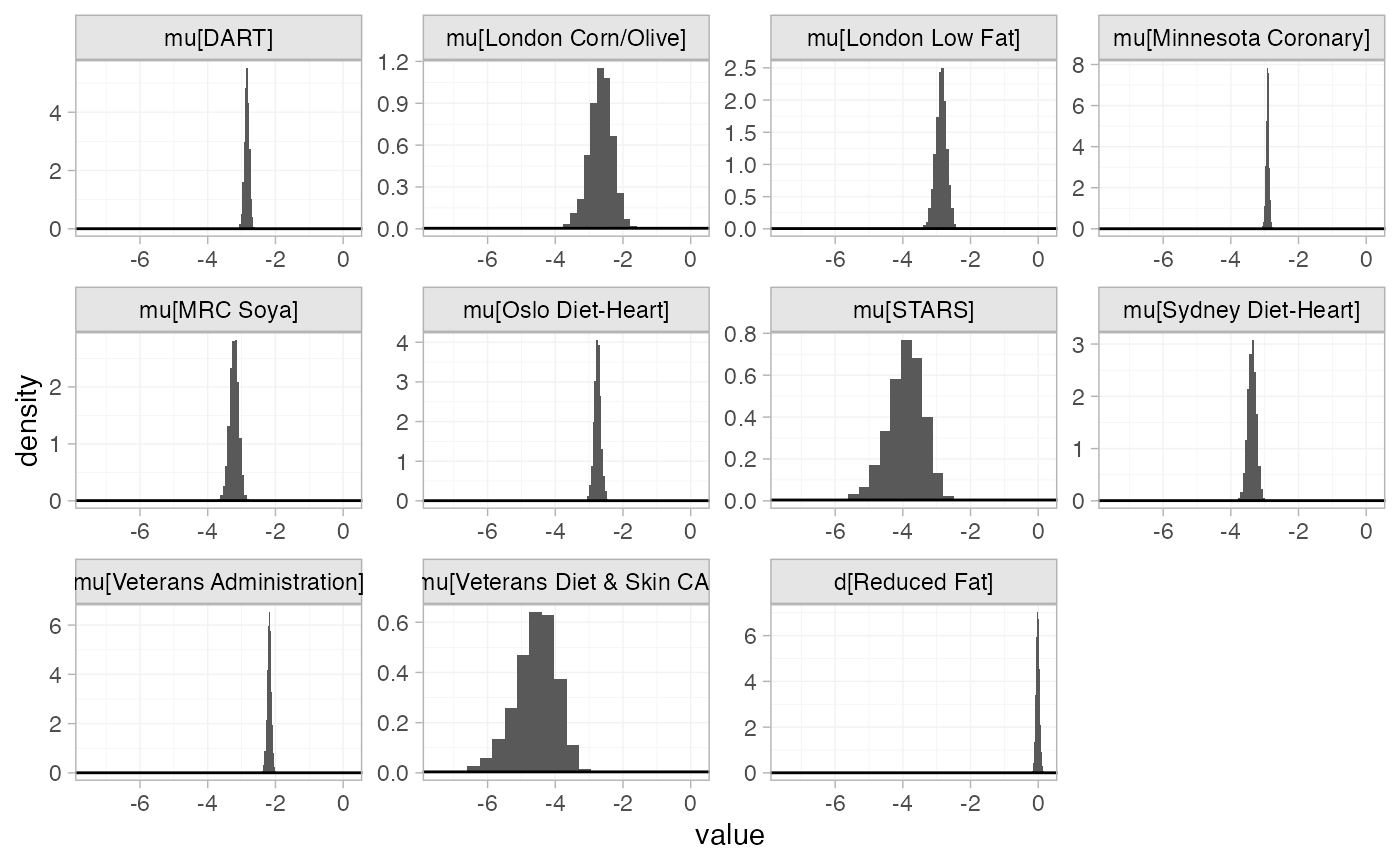

Random effects meta-analysis

We now fit a random effects model using the nma() function with trt_effects = "random". Again, we use $\mathrm{N}(0, 100^2)$ prior distributions for the treatment effects $d_k$ and study-specific intercepts $\mu_j$, and we additionally use a $\textrm{half-N}(5^2)$ prior for the heterogeneity standard deviation $\tau$. We can examine the range of parameter values implied by these prior distributions with the summary() method:

summary(normal(scale = 100))
#> A Normal prior distribution: location = 0, scale = 100.
#> 50% of the prior density lies between -67.45 and 67.45.
#> 95% of the prior density lies between -196 and 196.
summary(half_normal(scale = 5))
#> A half-Normal prior distribution: location = 0, scale = 5.
#> 50% of the prior density lies between 0 and 3.37.
#> 95% of the prior density lies between 0 and 9.8.

Fitting the RE model

diet_fit_RE <- nma(diet_net, 
                   trt_effects = "random",
                   prior_intercept = normal(scale = 100),
                   prior_trt = normal(scale = 100),
                   prior_het = half_normal(scale = 5))

#>  2000 [ 50%]  (Warmup)
#> Chain 2: Iteration: 1001 / 2000 [ 50%]  (Sampling)
#> Chain 3: Iteration: 1000 / 2000 [ 50%]  (Warmup)
#> Chain 3: Iteration: 1001 / 2000 [ 50%]  (Sampling)
#> Chain 3: Iteration: 1200 / 2000 [ 60%]  (Sampling)
#> Chain 2: Iteration: 1200 / 2000 [ 60%]  (Sampling)
#> Chain 1: Iteration: 1200 / 2000 [ 60%]  (Sampling)
#> Chain 3: Iteration: 1400 / 2000 [ 70%]  (Sampling)
#> Chain 2: Iteration: 1400 / 2000 [ 70%]  (Sampling)
#> Chain 1: Iteration: 1400 / 2000 [ 70%]  (Sampling)
#> Chain 3: Iteration: 1600 / 2000 [ 80%]  (Sampling)
#> Chain 2: Iteration: 1600 / 2000 [ 80%]  (Sampling)
#> Chain 1: Iteration: 1600 / 2000 [ 80%]  (Sampling)
#> Chain 3: Iteration: 1800 / 2000 [ 90%]  (Sampling)
#> Chain 2: Iteration: 1800 / 2000 [ 90%]  (Sampling)
#> Chain 1: Iteration: 1800 / 2000 [ 90%]  (Sampling)
#> Chain 3: Iteration: 2000 / 2000 [100%]  (Sampling)
#> Chain 3: 
#> Chain 3:  Elapsed Time: 0.198 seconds (Warm-up)
#> Chain 3:                0.156 seconds (Sampling)
#> Chain 3:                0.354 seconds (Total)
#> Chain 3: 
#> Chain 2: Iteration: 2000 / 2000 [100%]  (Sampling)
#> Chain 2: 
#> Chain 2:  Elapsed Time: 0.206 seconds (Warm-up)
#> Chain 2:                0.159 seconds (Sampling)
#> Chain 2:                0.365 seconds (Total)
#> Chain 2: 
#> Chain 1: Iteration: 2000 / 2000 [100%]  (Sampling)
#> Chain 1: 
#> Chain 1:  Elapsed Time: 0.198 seconds (Warm-up)
#> Chain 1:                0.169 seconds (Sampling)
#> Chain 1:                0.367 seconds (Total)
#> Chain 1:

Basic parameter summaries are given by the print() method:

diet_fit_RE
#> A random effects NMA with a poisson likelihood (log link).
#> Inference for Stan model: poisson.
#> 4 chains, each with iter=2000; warmup=1000; thin=1; 
#> post-warmup draws per chain=1000, total post-warmup draws=4000.
#> 
#>                   mean se_mean   sd    2.5%     25%     50%     75%   97.5% n_eff Rhat
#> d[Reduced Fat]   -0.02    0.00 0.09   -0.19   -0.06   -0.02    0.03    0.15  1581    1
#> lp__           5379.23    0.11 3.74 5371.41 5376.76 5379.38 5381.88 5385.92  1217    1
#> tau               0.13    0.00 0.12    0.01    0.05    0.10    0.18    0.45   819    1
#> 
#> Samples were drawn using NUTS(diag_e) at Tue Sep 24 09:06:24 2024.
#> For each parameter, n_eff is a crude measure of effective sample size,
#> and Rhat is the potential scale reduction factor on split chains (at 
#> convergence, Rhat=1).

By default, summaries of the study-specific intercepts $\mu_j$ and study-specific relative effects $\delta_{jk}$ are hidden, but could be examined by changing the pars argument:

# Not run
print(diet_fit_RE, pars = c("d", "mu", "delta"))

The prior and posterior distributions can be compared visually using the plot_prior_posterior() function:

plot_prior_posterior(diet_fit_RE, prior = c("trt", "het"))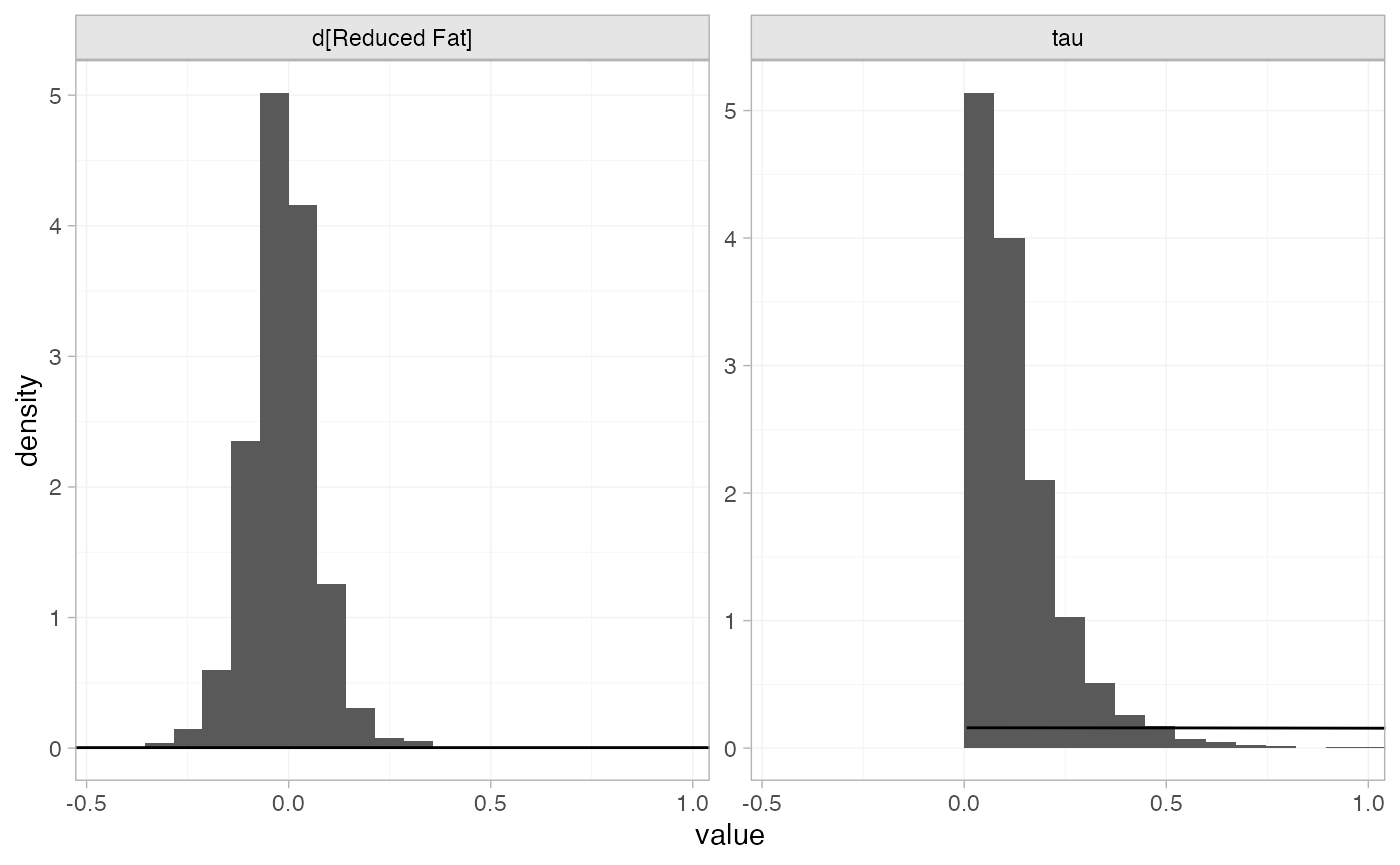

Model comparison

Model fit can be checked using the dic() function:

(dic_FE <- dic(diet_fit_FE))
#> Residual deviance: 22.5 (on 21 data points)
#>                pD: 11.3
#>               DIC: 33.8

(dic_RE <- dic(diet_fit_RE))
#> Residual deviance: 21.4 (on 21 data points)
#>                pD: 13.5
#>               DIC: 34.9

Both models appear to fit the data well, as the residual deviance is close to the number of data points. The DIC is very similar between models, so the FE model may be preferred for parsimony.

We can also examine the residual deviance contributions with the corresponding plot() method.

plot(dic_FE)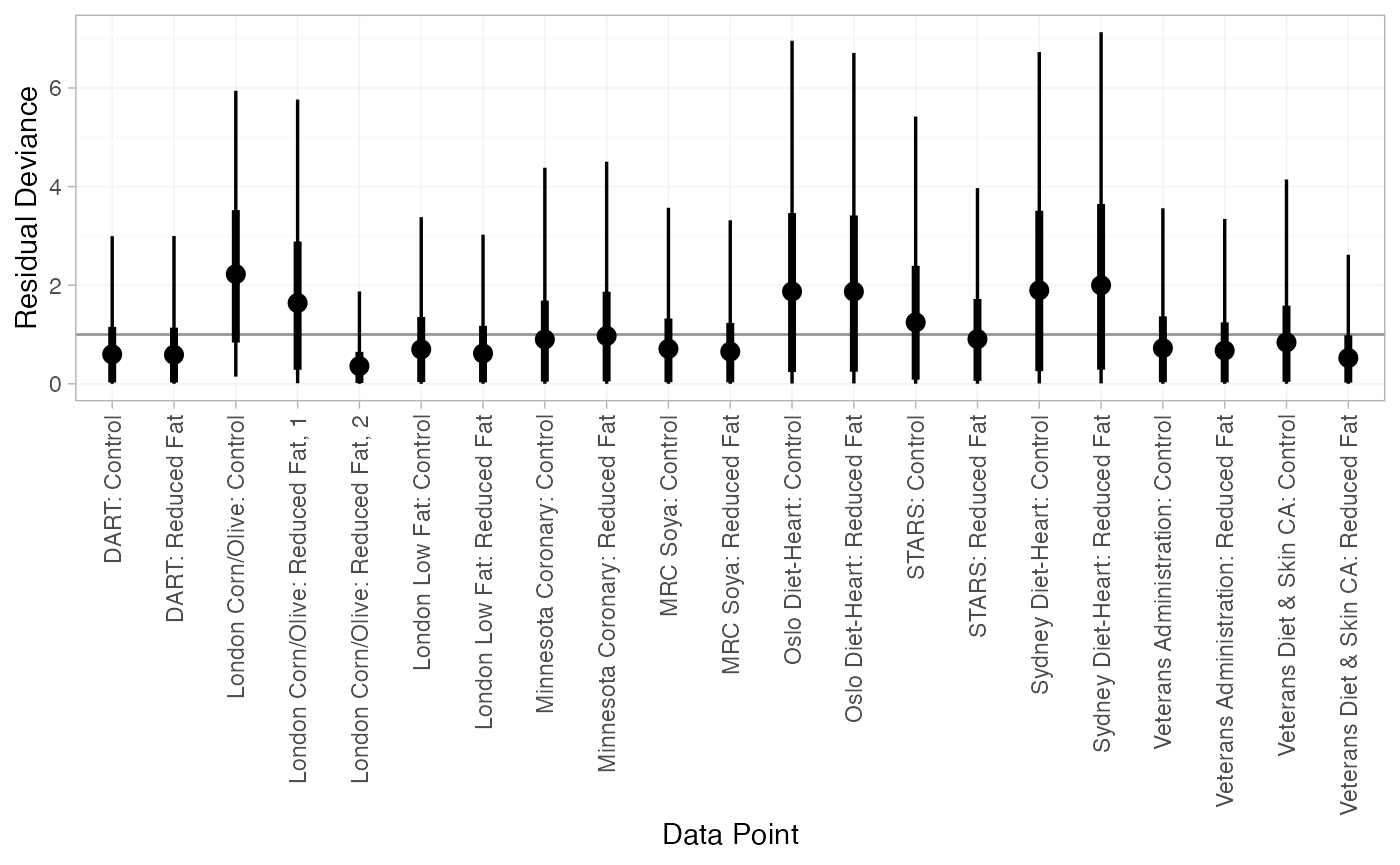

plot(dic_RE)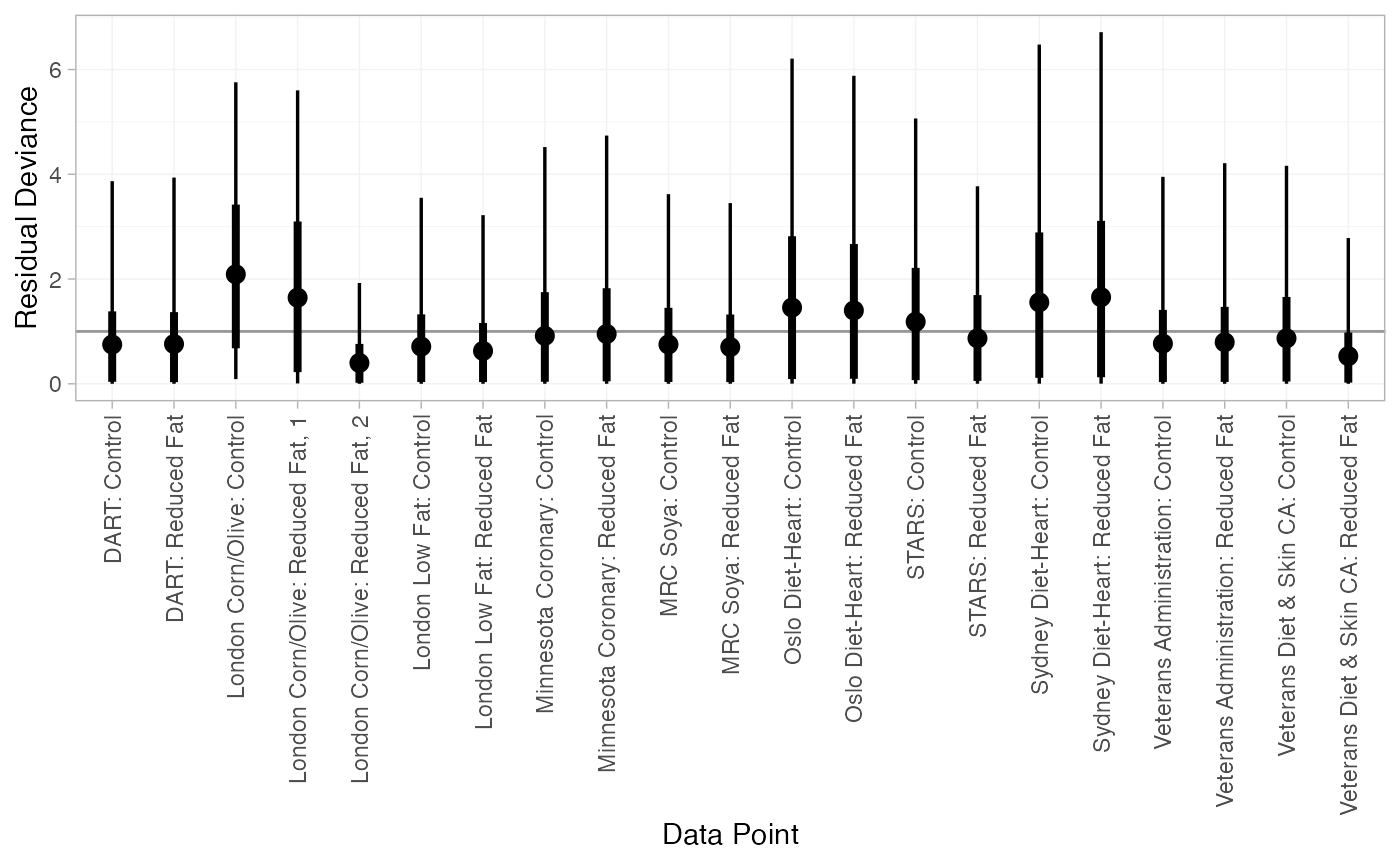

Further results

Dias et al. (2011) produce absolute predictions of the mortality rates on reduced fat and control diets, assuming a Normal distribution on the baseline log rate of mortality with mean $-3$ and precision $1.77$. We can replicate these results using the predict() method. The baseline argument takes a distr() distribution object, with which we specify the corresponding Normal distribution. We set type = "response" to produce predicted rates (type = "link" would produce predicted log rates).

pred_FE <- predict(diet_fit_FE, 
                   baseline = distr(qnorm, mean = -3, sd = 1.77^-0.5), 
                   type = "response")
pred_FE
#>                   mean   sd 2.5%  25%  50%  75% 97.5% Bulk_ESS Tail_ESS Rhat
#> pred[Control]     0.06 0.05 0.01 0.03 0.05 0.08  0.21     4142     3904    1
#> pred[Reduced Fat] 0.06 0.05 0.01 0.03 0.05 0.08  0.21     4118     3909    1
plot(pred_FE)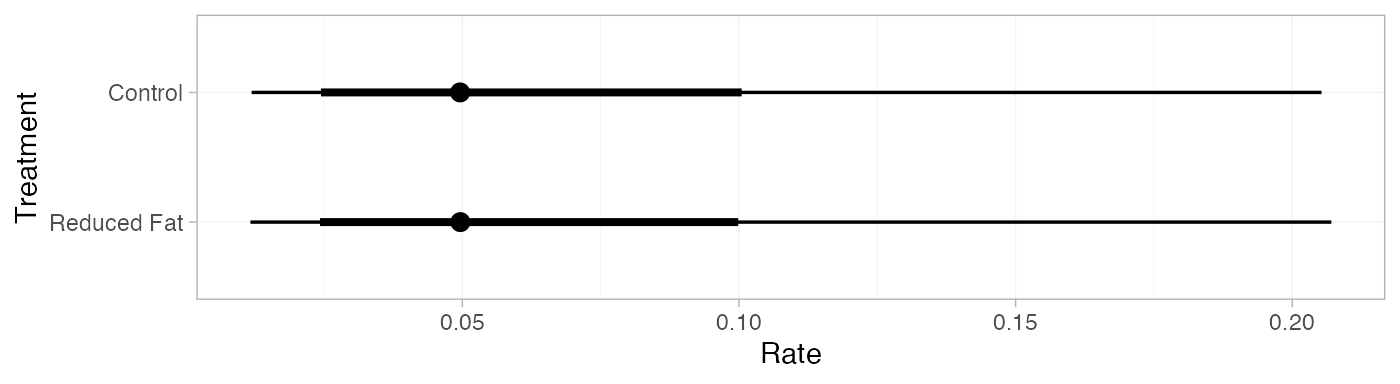

pred_RE <- predict(diet_fit_RE, 
                   baseline = distr(qnorm, mean = -3, sd = 1.77^-0.5), 
                   type = "response")
pred_RE
#>                   mean   sd 2.5%  25%  50%  75% 97.5% Bulk_ESS Tail_ESS Rhat
#> pred[Control]     0.07 0.06 0.01 0.03 0.05 0.08  0.22     4379     3576    1
#> pred[Reduced Fat] 0.07 0.06 0.01 0.03 0.05 0.08  0.21     4394     3531    1
plot(pred_RE)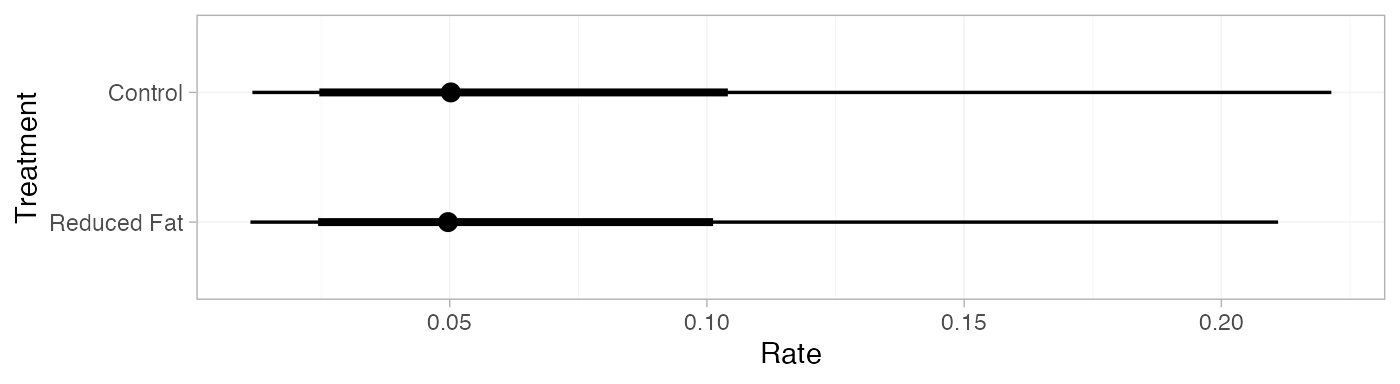

If the baseline argument is omitted, predicted rates will be produced for every study in the network based on their estimated baseline log rate $\mu_j$:

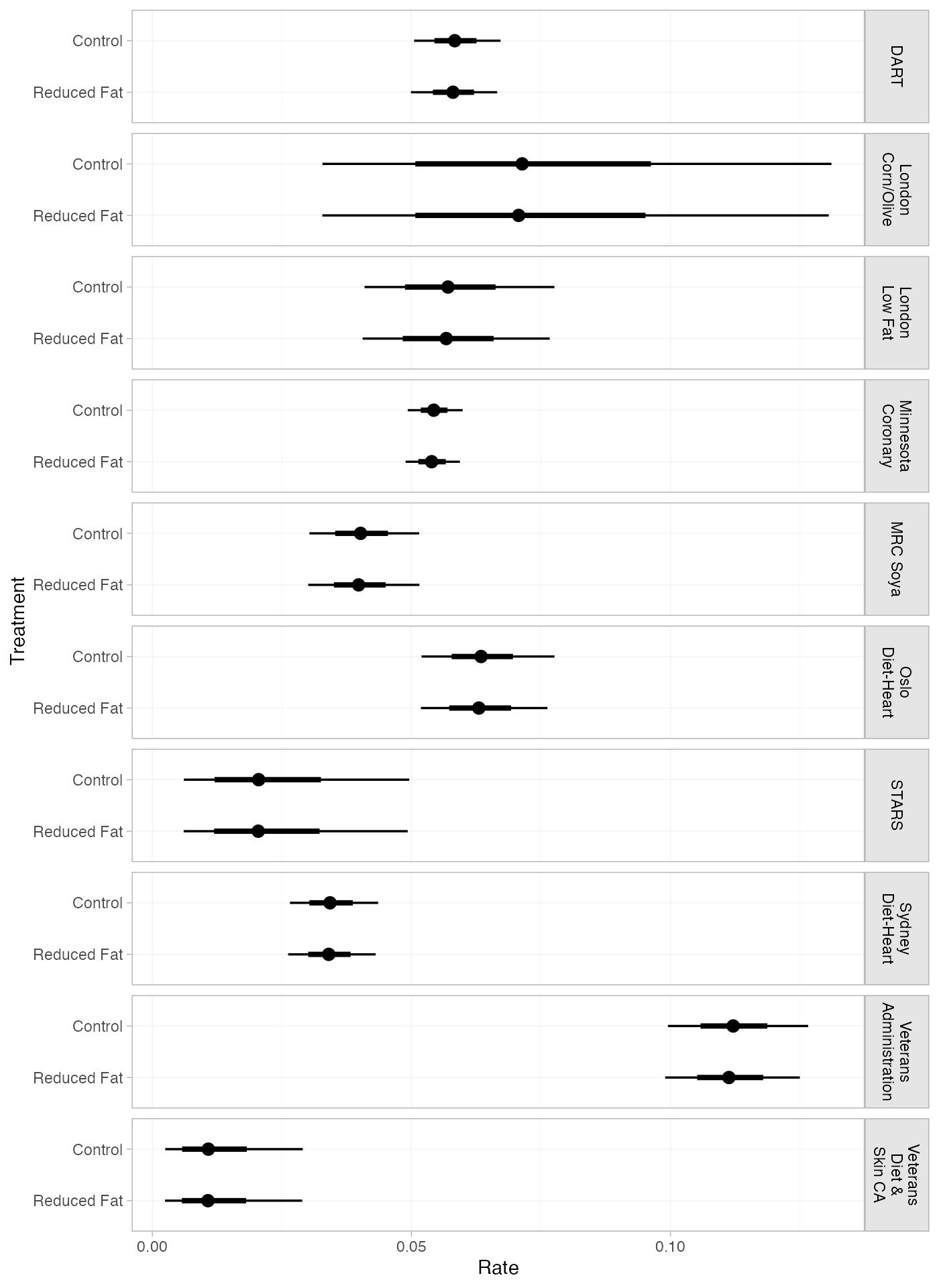
pred_FE_studies <- predict(diet_fit_FE, type = "response")
pred_FE_studies
#> ------------------------------------------------------------------- Study: DART ---- 
#> 
#>                         mean sd 2.5%  25%  50%  75% 97.5% Bulk_ESS Tail_ESS Rhat
#> pred[DART: Control]     0.06  0 0.05 0.06 0.06 0.06  0.07     6187     3190    1
#> pred[DART: Reduced Fat] 0.06  0 0.05 0.06 0.06 0.06  0.07     7818     3376    1
#> 
#> ------------------------------------------------------ Study: London Corn/Olive ---- 
#> 
#>                                      mean   sd 2.5%  25%  50%  75% 97.5% Bulk_ESS Tail_ESS
#> pred[London Corn/Olive: Control]     0.07 0.03 0.03 0.06 0.07 0.09  0.13     8422     3035
#> pred[London Corn/Olive: Reduced Fat] 0.07 0.02 0.03 0.06 0.07 0.09  0.13     8512     3110
#>                                      Rhat
#> pred[London Corn/Olive: Control]        1
#> pred[London Corn/Olive: Reduced Fat]    1
#> 
#> --------------------------------------------------------- Study: London Low Fat ---- 
#> 
#>                                   mean   sd 2.5%  25%  50%  75% 97.5% Bulk_ESS Tail_ESS Rhat
#> pred[London Low Fat: Control]     0.06 0.01 0.04 0.05 0.06 0.06  0.08     7697     2749    1
#> pred[London Low Fat: Reduced Fat] 0.06 0.01 0.04 0.05 0.06 0.06  0.08     8588     2715    1
#> 
#> ----------------------------------------------------- Study: Minnesota Coronary ---- 
#> 
#>                                       mean sd 2.5%  25%  50%  75% 97.5% Bulk_ESS Tail_ESS Rhat
#> pred[Minnesota Coronary: Control]     0.05  0 0.05 0.05 0.05 0.06  0.06     5035     3586    1
#> pred[Minnesota Coronary: Reduced Fat] 0.05  0 0.05 0.05 0.05 0.06  0.06     6263     3698    1
#> 
#> --------------------------------------------------------------- Study: MRC Soya ---- 
#> 
#>                             mean   sd 2.5%  25%  50%  75% 97.5% Bulk_ESS Tail_ESS Rhat
#> pred[MRC Soya: Control]     0.04 0.01 0.03 0.04 0.04 0.04  0.05     7530     2448    1
#> pred[MRC Soya: Reduced Fat] 0.04 0.01 0.03 0.04 0.04 0.04  0.05     8515     2983    1
#> 
#> -------------------------------------------------------- Study: Oslo Diet-Heart ---- 
#> 
#>                                    mean   sd 2.5%  25%  50%  75% 97.5% Bulk_ESS Tail_ESS Rhat
#> pred[Oslo Diet-Heart: Control]     0.06 0.01 0.05 0.06 0.06 0.07  0.08     6664     3113    1
#> pred[Oslo Diet-Heart: Reduced Fat] 0.06 0.01 0.05 0.06 0.06 0.07  0.08     8209     3279    1
#> 
#> ------------------------------------------------------------------ Study: STARS ---- 
#> 
#>                          mean   sd 2.5%  25%  50%  75% 97.5% Bulk_ESS Tail_ESS Rhat
#> pred[STARS: Control]     0.02 0.01 0.01 0.01 0.02 0.03  0.05     6720     2887    1
#> pred[STARS: Reduced Fat] 0.02 0.01 0.01 0.01 0.02 0.03  0.05     6802     2867    1
#> 
#> ------------------------------------------------------ Study: Sydney Diet-Heart ---- 
#> 
#>                                      mean sd 2.5%  25%  50%  75% 97.5% Bulk_ESS Tail_ESS Rhat
#> pred[Sydney Diet-Heart: Control]     0.03  0 0.03 0.03 0.03 0.04  0.04     7106     2707    1
#> pred[Sydney Diet-Heart: Reduced Fat] 0.03  0 0.03 0.03 0.03 0.04  0.04     7635     2816    1
#> 
#> ------------------------------------------------ Study: Veterans Administration ---- 
#> 
#>                                            mean   sd 2.5%  25%  50%  75% 97.5% Bulk_ESS
#> pred[Veterans Administration: Control]     0.11 0.01  0.1 0.11 0.11 0.12  0.13     5091
#> pred[Veterans Administration: Reduced Fat] 0.11 0.01  0.1 0.11 0.11 0.12  0.12     6910
#>                                            Tail_ESS Rhat
#> pred[Veterans Administration: Control]         3139    1
#> pred[Veterans Administration: Reduced Fat]     3250    1
#> 
#> ------------------------------------------------ Study: Veterans Diet & Skin CA ---- 
#> 
#>                                            mean   sd 2.5%  25%  50%  75% 97.5% Bulk_ESS
#> pred[Veterans Diet & Skin CA: Control]     0.01 0.01    0 0.01 0.01 0.02  0.03     5371
#> pred[Veterans Diet & Skin CA: Reduced Fat] 0.01 0.01    0 0.01 0.01 0.02  0.03     5342
#>                                            Tail_ESS Rhat
#> pred[Veterans Diet & Skin CA: Control]         2466    1
#> pred[Veterans Diet & Skin CA: Reduced Fat]     2556    1
plot(pred_FE_studies) + ggplot2::facet_grid(Study~., labeller = ggplot2::label_wrap_gen(width = 10))

References

Dias, S., N. J. Welton, A. J. Sutton, and A. E. Ades. 2011. “NICE DSU Technical Support Document 2: A Generalised Linear Modelling Framework for Pair-Wise and Network Meta-Analysis of Randomised Controlled Trials.” National Institute for Health and Care Excellence. https://www.sheffield.ac.uk/nice-dsu.

Hooper, L., C. D. Summerbell, J. P. T. Higgins, R. L. Thompson, G. Clements, N. Capps, G. Davey Smith, R. Riemersma, and S. Ebrahim. 2000. “Reduced or Modified Dietary Fat for Preventing Cardiovascular Disease.” Cochrane Database of Systematic Reviews, no. 2. https://doi.org/10.1002/14651858.CD002137.