Produce posterior treatment rankings and rank probabilities from a fitted NMA model. When a meta-regression is fitted with effect modifier interactions with treatment, these will differ by study population.
Usage
posterior_ranks(
x,
newdata = NULL,
study = NULL,
lower_better = TRUE,
probs = c(0.025, 0.25, 0.5, 0.75, 0.975),
sucra = FALSE,
summary = TRUE
)
posterior_rank_probs(
x,
newdata = NULL,
study = NULL,
lower_better = TRUE,
cumulative = FALSE,
sucra = FALSE
)Arguments
- x
A
stan_nmaobject created bynma()- newdata
Only used if a regression model is fitted. A data frame of study details, one row per study, giving the covariate values at which to produce relative effects. Column names must match variables in the regression model. If
NULL, relative effects are produced for all studies in the network.- study
Column of
newdatawhich specifies study names, otherwise studies will be labelled by row number.- lower_better
Logical, are lower treatment effects better (
TRUE; default) or higher better (FALSE)? See details.- probs
Numeric vector of quantiles of interest to present in computed summary, default
c(0.025, 0.25, 0.5, 0.75, 0.975)- sucra
Logical, calculate the surface under the cumulative ranking curve (SUCRA) for each treatment? Default
FALSE.- summary
Logical, calculate posterior summaries? Default
TRUE.- cumulative
Logical, return cumulative rank probabilities? Default is
FALSE, return posterior probabilities of each treatment having a given rank. IfTRUE, cumulative posterior rank probabilities are returned for each treatment having a given rank or better.
Value
A nma_summary object if summary = TRUE, otherwise a list
containing a 3D MCMC array of samples and (for regression models) a data
frame of study information.
Details
The function posterior_ranks() produces posterior rankings, which
have a distribution (e.g. mean/median rank and 95% Credible Interval). The
function posterior_rank_probs() produces rank probabilities, which give
the posterior probabilities of being ranked first, second, etc. out of all
treatments.
The argument lower_better specifies whether lower treatment
effects or higher treatment effects are preferred. For example, with a
negative binary outcome lower (more negative) log odds ratios are
preferred, so lower_better = TRUE. Conversely, for example, if treatments
aim to increase the rate of a positive outcome then lower_better = FALSE.
See also
plot.nma_summary() for plotting the ranks and rank probabilities.
Examples
## Smoking cessation
# \donttest{
# Run smoking RE NMA example if not already available
if (!exists("smk_fit_RE")) example("example_smk_re", run.donttest = TRUE)
# }
# \donttest{
# Produce posterior ranks
smk_rank_RE <- posterior_ranks(smk_fit_RE, lower_better = FALSE)
smk_rank_RE
#> mean sd 2.5% 25% 50% 75% 97.5% Bulk_ESS Tail_ESS
#> rank[No intervention] 3.90 0.31 3 4 4 4 4 2381 NA
#> rank[Group counselling] 1.37 0.62 1 1 1 2 3 2812 2553
#> rank[Individual counselling] 1.93 0.64 1 2 2 2 3 2474 2625
#> rank[Self-help] 2.80 0.68 1 3 3 3 4 2517 NA
#> Rhat
#> rank[No intervention] 1
#> rank[Group counselling] 1
#> rank[Individual counselling] 1
#> rank[Self-help] 1
plot(smk_rank_RE)
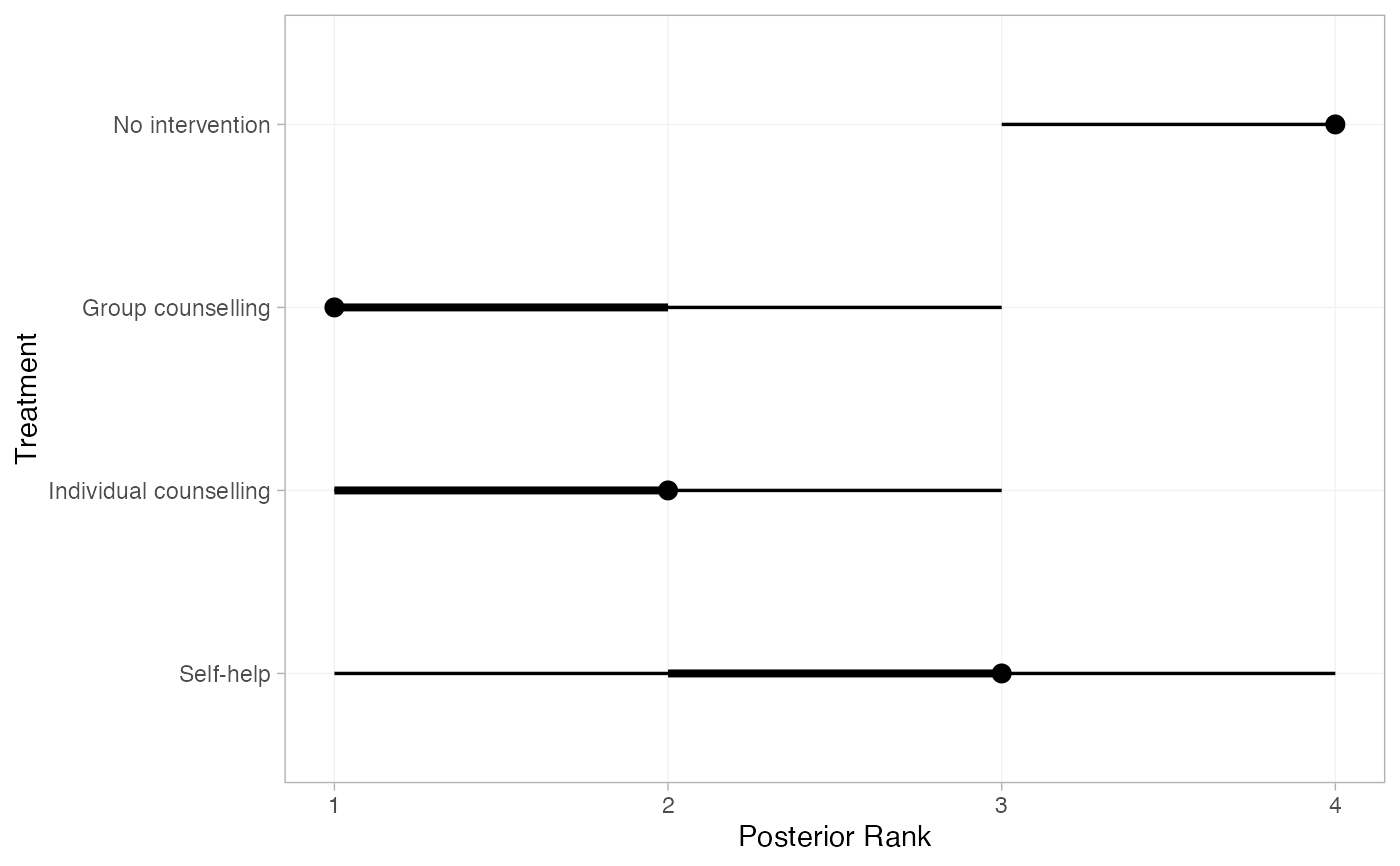 # Produce rank probabilities
smk_rankprob_RE <- posterior_rank_probs(smk_fit_RE, lower_better = FALSE)
smk_rankprob_RE
#> p_rank[1] p_rank[2] p_rank[3] p_rank[4]
#> d[No intervention] 0.00 0.00 0.10 0.90
#> d[Group counselling] 0.70 0.23 0.06 0.01
#> d[Individual counselling] 0.24 0.59 0.17 0.00
#> d[Self-help] 0.06 0.18 0.67 0.10
plot(smk_rankprob_RE)
# Produce rank probabilities
smk_rankprob_RE <- posterior_rank_probs(smk_fit_RE, lower_better = FALSE)
smk_rankprob_RE
#> p_rank[1] p_rank[2] p_rank[3] p_rank[4]
#> d[No intervention] 0.00 0.00 0.10 0.90
#> d[Group counselling] 0.70 0.23 0.06 0.01
#> d[Individual counselling] 0.24 0.59 0.17 0.00
#> d[Self-help] 0.06 0.18 0.67 0.10
plot(smk_rankprob_RE)
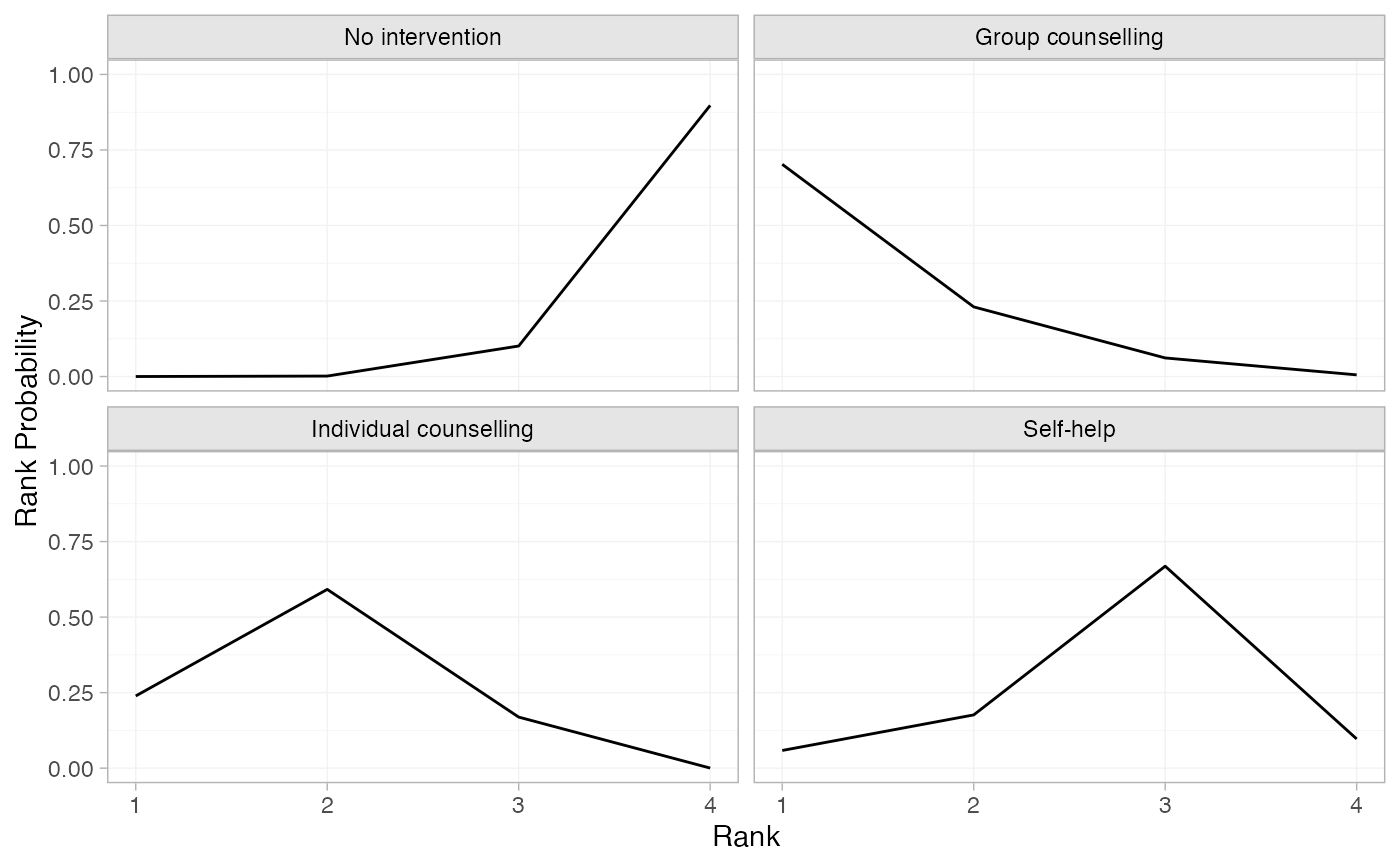 # Produce cumulative rank probabilities
smk_cumrankprob_RE <- posterior_rank_probs(smk_fit_RE, lower_better = FALSE,
cumulative = TRUE)
smk_cumrankprob_RE
#> p_rank[1] p_rank[2] p_rank[3] p_rank[4]
#> d[No intervention] 0.00 0.00 0.10 1
#> d[Group counselling] 0.70 0.93 0.99 1
#> d[Individual counselling] 0.24 0.83 1.00 1
#> d[Self-help] 0.06 0.23 0.90 1
plot(smk_cumrankprob_RE)
# Produce cumulative rank probabilities
smk_cumrankprob_RE <- posterior_rank_probs(smk_fit_RE, lower_better = FALSE,
cumulative = TRUE)
smk_cumrankprob_RE
#> p_rank[1] p_rank[2] p_rank[3] p_rank[4]
#> d[No intervention] 0.00 0.00 0.10 1
#> d[Group counselling] 0.70 0.93 0.99 1
#> d[Individual counselling] 0.24 0.83 1.00 1
#> d[Self-help] 0.06 0.23 0.90 1
plot(smk_cumrankprob_RE)
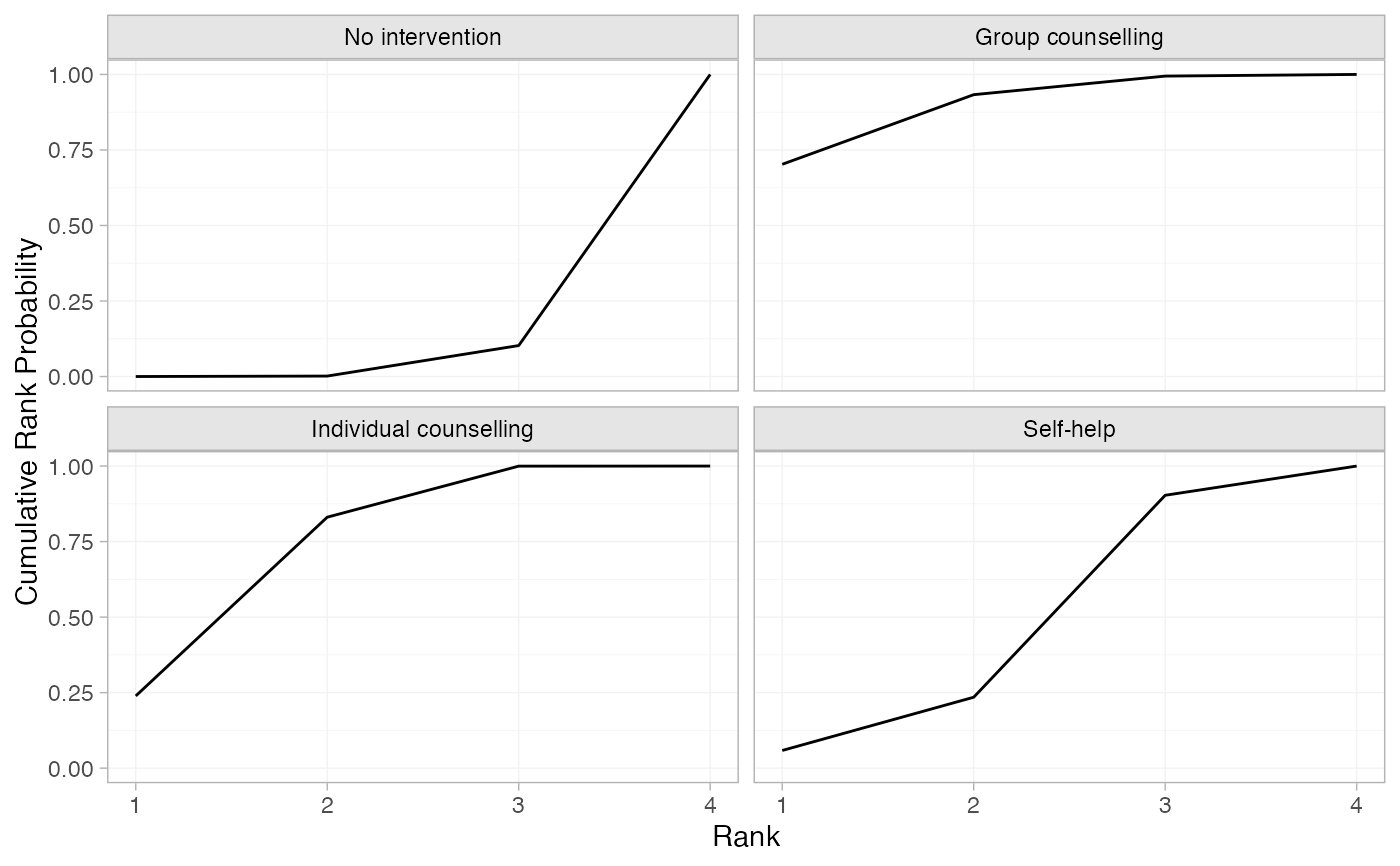 # Further customisation is possible with ggplot commands
plot(smk_cumrankprob_RE) +
ggplot2::facet_null() +
ggplot2::aes(colour = Treatment)
# Further customisation is possible with ggplot commands
plot(smk_cumrankprob_RE) +
ggplot2::facet_null() +
ggplot2::aes(colour = Treatment)
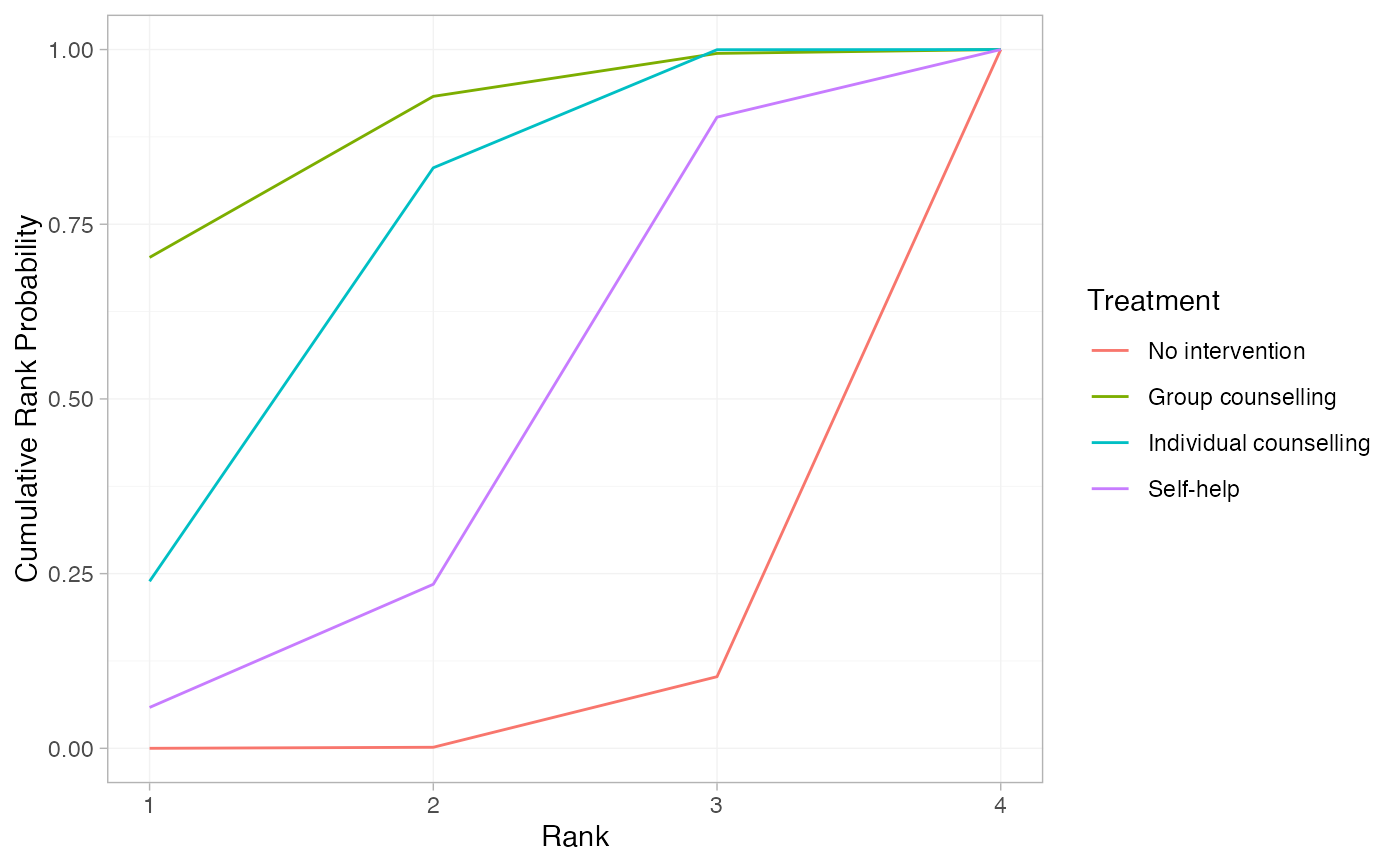 # }
## Plaque psoriasis ML-NMR
# \donttest{
# Run plaque psoriasis ML-NMR example if not already available
if (!exists("pso_fit")) example("example_pso_mlnmr", run.donttest = TRUE)
# }
# \donttest{
# Produce population-adjusted rankings for all study populations in
# the network
# Ranks
pso_rank <- posterior_ranks(pso_fit)
pso_rank
#> ---------------------------------------------------------------- Study: FIXTURE ----
#>
#> Covariate values:
#> durnpso prevsys bsa weight psa
#> 1.6 0.62 0.34 8.34 0.14
#>
#> mean sd 2.5% 25% 50% 75% 97.5% Bulk_ESS Tail_ESS Rhat
#> rank[FIXTURE: PBO] 1.00 0.00 1 1 1 1 1 NA NA NA
#> rank[FIXTURE: ETN] 2.00 0.00 2 2 2 2 2 NA NA NA
#> rank[FIXTURE: IXE_Q2W] 6.00 0.00 6 6 6 6 6 NA NA NA
#> rank[FIXTURE: IXE_Q4W] 4.78 0.41 4 5 5 5 5 4047 NA 1
#> rank[FIXTURE: SEC_150] 3.00 0.05 3 3 3 3 3 3397 3397 1
#> rank[FIXTURE: SEC_300] 4.22 0.42 4 4 4 4 5 4130 NA 1
#>
#> -------------------------------------------------------------- Study: UNCOVER-1 ----
#>
#> Covariate values:
#> durnpso prevsys bsa weight psa
#> 2 0.73 0.28 9.24 0.28
#>
#> mean sd 2.5% 25% 50% 75% 97.5% Bulk_ESS Tail_ESS
#> rank[UNCOVER-1: PBO] 1.00 0.00 1 1 1 1 1 NA NA
#> rank[UNCOVER-1: ETN] 2.00 0.00 2 2 2 2 2 NA NA
#> rank[UNCOVER-1: IXE_Q2W] 6.00 0.00 6 6 6 6 6 NA NA
#> rank[UNCOVER-1: IXE_Q4W] 4.78 0.41 4 5 5 5 5 4047 NA
#> rank[UNCOVER-1: SEC_150] 3.00 0.05 3 3 3 3 3 3397 3397
#> rank[UNCOVER-1: SEC_300] 4.22 0.42 4 4 4 4 5 4130 NA
#> Rhat
#> rank[UNCOVER-1: PBO] NA
#> rank[UNCOVER-1: ETN] NA
#> rank[UNCOVER-1: IXE_Q2W] NA
#> rank[UNCOVER-1: IXE_Q4W] 1
#> rank[UNCOVER-1: SEC_150] 1
#> rank[UNCOVER-1: SEC_300] 1
#>
#> -------------------------------------------------------------- Study: UNCOVER-2 ----
#>
#> Covariate values:
#> durnpso prevsys bsa weight psa
#> 1.87 0.64 0.27 9.17 0.24
#>
#> mean sd 2.5% 25% 50% 75% 97.5% Bulk_ESS Tail_ESS
#> rank[UNCOVER-2: PBO] 1.00 0.00 1 1 1 1 1 NA NA
#> rank[UNCOVER-2: ETN] 2.00 0.00 2 2 2 2 2 NA NA
#> rank[UNCOVER-2: IXE_Q2W] 6.00 0.00 6 6 6 6 6 NA NA
#> rank[UNCOVER-2: IXE_Q4W] 4.78 0.41 4 5 5 5 5 4047 NA
#> rank[UNCOVER-2: SEC_150] 3.00 0.05 3 3 3 3 3 3397 3397
#> rank[UNCOVER-2: SEC_300] 4.22 0.42 4 4 4 4 5 4130 NA
#> Rhat
#> rank[UNCOVER-2: PBO] NA
#> rank[UNCOVER-2: ETN] NA
#> rank[UNCOVER-2: IXE_Q2W] NA
#> rank[UNCOVER-2: IXE_Q4W] 1
#> rank[UNCOVER-2: SEC_150] 1
#> rank[UNCOVER-2: SEC_300] 1
#>
#> -------------------------------------------------------------- Study: UNCOVER-3 ----
#>
#> Covariate values:
#> durnpso prevsys bsa weight psa
#> 1.78 0.59 0.28 9.01 0.2
#>
#> mean sd 2.5% 25% 50% 75% 97.5% Bulk_ESS Tail_ESS
#> rank[UNCOVER-3: PBO] 1.00 0.00 1 1 1 1 1 NA NA
#> rank[UNCOVER-3: ETN] 2.00 0.00 2 2 2 2 2 NA NA
#> rank[UNCOVER-3: IXE_Q2W] 6.00 0.00 6 6 6 6 6 NA NA
#> rank[UNCOVER-3: IXE_Q4W] 4.78 0.41 4 5 5 5 5 4047 NA
#> rank[UNCOVER-3: SEC_150] 3.00 0.05 3 3 3 3 3 3397 3397
#> rank[UNCOVER-3: SEC_300] 4.22 0.42 4 4 4 4 5 4130 NA
#> Rhat
#> rank[UNCOVER-3: PBO] NA
#> rank[UNCOVER-3: ETN] NA
#> rank[UNCOVER-3: IXE_Q2W] NA
#> rank[UNCOVER-3: IXE_Q4W] 1
#> rank[UNCOVER-3: SEC_150] 1
#> rank[UNCOVER-3: SEC_300] 1
#>
plot(pso_rank)
# }
## Plaque psoriasis ML-NMR
# \donttest{
# Run plaque psoriasis ML-NMR example if not already available
if (!exists("pso_fit")) example("example_pso_mlnmr", run.donttest = TRUE)
# }
# \donttest{
# Produce population-adjusted rankings for all study populations in
# the network
# Ranks
pso_rank <- posterior_ranks(pso_fit)
pso_rank
#> ---------------------------------------------------------------- Study: FIXTURE ----
#>
#> Covariate values:
#> durnpso prevsys bsa weight psa
#> 1.6 0.62 0.34 8.34 0.14
#>
#> mean sd 2.5% 25% 50% 75% 97.5% Bulk_ESS Tail_ESS Rhat
#> rank[FIXTURE: PBO] 1.00 0.00 1 1 1 1 1 NA NA NA
#> rank[FIXTURE: ETN] 2.00 0.00 2 2 2 2 2 NA NA NA
#> rank[FIXTURE: IXE_Q2W] 6.00 0.00 6 6 6 6 6 NA NA NA
#> rank[FIXTURE: IXE_Q4W] 4.78 0.41 4 5 5 5 5 4047 NA 1
#> rank[FIXTURE: SEC_150] 3.00 0.05 3 3 3 3 3 3397 3397 1
#> rank[FIXTURE: SEC_300] 4.22 0.42 4 4 4 4 5 4130 NA 1
#>
#> -------------------------------------------------------------- Study: UNCOVER-1 ----
#>
#> Covariate values:
#> durnpso prevsys bsa weight psa
#> 2 0.73 0.28 9.24 0.28
#>
#> mean sd 2.5% 25% 50% 75% 97.5% Bulk_ESS Tail_ESS
#> rank[UNCOVER-1: PBO] 1.00 0.00 1 1 1 1 1 NA NA
#> rank[UNCOVER-1: ETN] 2.00 0.00 2 2 2 2 2 NA NA
#> rank[UNCOVER-1: IXE_Q2W] 6.00 0.00 6 6 6 6 6 NA NA
#> rank[UNCOVER-1: IXE_Q4W] 4.78 0.41 4 5 5 5 5 4047 NA
#> rank[UNCOVER-1: SEC_150] 3.00 0.05 3 3 3 3 3 3397 3397
#> rank[UNCOVER-1: SEC_300] 4.22 0.42 4 4 4 4 5 4130 NA
#> Rhat
#> rank[UNCOVER-1: PBO] NA
#> rank[UNCOVER-1: ETN] NA
#> rank[UNCOVER-1: IXE_Q2W] NA
#> rank[UNCOVER-1: IXE_Q4W] 1
#> rank[UNCOVER-1: SEC_150] 1
#> rank[UNCOVER-1: SEC_300] 1
#>
#> -------------------------------------------------------------- Study: UNCOVER-2 ----
#>
#> Covariate values:
#> durnpso prevsys bsa weight psa
#> 1.87 0.64 0.27 9.17 0.24
#>
#> mean sd 2.5% 25% 50% 75% 97.5% Bulk_ESS Tail_ESS
#> rank[UNCOVER-2: PBO] 1.00 0.00 1 1 1 1 1 NA NA
#> rank[UNCOVER-2: ETN] 2.00 0.00 2 2 2 2 2 NA NA
#> rank[UNCOVER-2: IXE_Q2W] 6.00 0.00 6 6 6 6 6 NA NA
#> rank[UNCOVER-2: IXE_Q4W] 4.78 0.41 4 5 5 5 5 4047 NA
#> rank[UNCOVER-2: SEC_150] 3.00 0.05 3 3 3 3 3 3397 3397
#> rank[UNCOVER-2: SEC_300] 4.22 0.42 4 4 4 4 5 4130 NA
#> Rhat
#> rank[UNCOVER-2: PBO] NA
#> rank[UNCOVER-2: ETN] NA
#> rank[UNCOVER-2: IXE_Q2W] NA
#> rank[UNCOVER-2: IXE_Q4W] 1
#> rank[UNCOVER-2: SEC_150] 1
#> rank[UNCOVER-2: SEC_300] 1
#>
#> -------------------------------------------------------------- Study: UNCOVER-3 ----
#>
#> Covariate values:
#> durnpso prevsys bsa weight psa
#> 1.78 0.59 0.28 9.01 0.2
#>
#> mean sd 2.5% 25% 50% 75% 97.5% Bulk_ESS Tail_ESS
#> rank[UNCOVER-3: PBO] 1.00 0.00 1 1 1 1 1 NA NA
#> rank[UNCOVER-3: ETN] 2.00 0.00 2 2 2 2 2 NA NA
#> rank[UNCOVER-3: IXE_Q2W] 6.00 0.00 6 6 6 6 6 NA NA
#> rank[UNCOVER-3: IXE_Q4W] 4.78 0.41 4 5 5 5 5 4047 NA
#> rank[UNCOVER-3: SEC_150] 3.00 0.05 3 3 3 3 3 3397 3397
#> rank[UNCOVER-3: SEC_300] 4.22 0.42 4 4 4 4 5 4130 NA
#> Rhat
#> rank[UNCOVER-3: PBO] NA
#> rank[UNCOVER-3: ETN] NA
#> rank[UNCOVER-3: IXE_Q2W] NA
#> rank[UNCOVER-3: IXE_Q4W] 1
#> rank[UNCOVER-3: SEC_150] 1
#> rank[UNCOVER-3: SEC_300] 1
#>
plot(pso_rank)
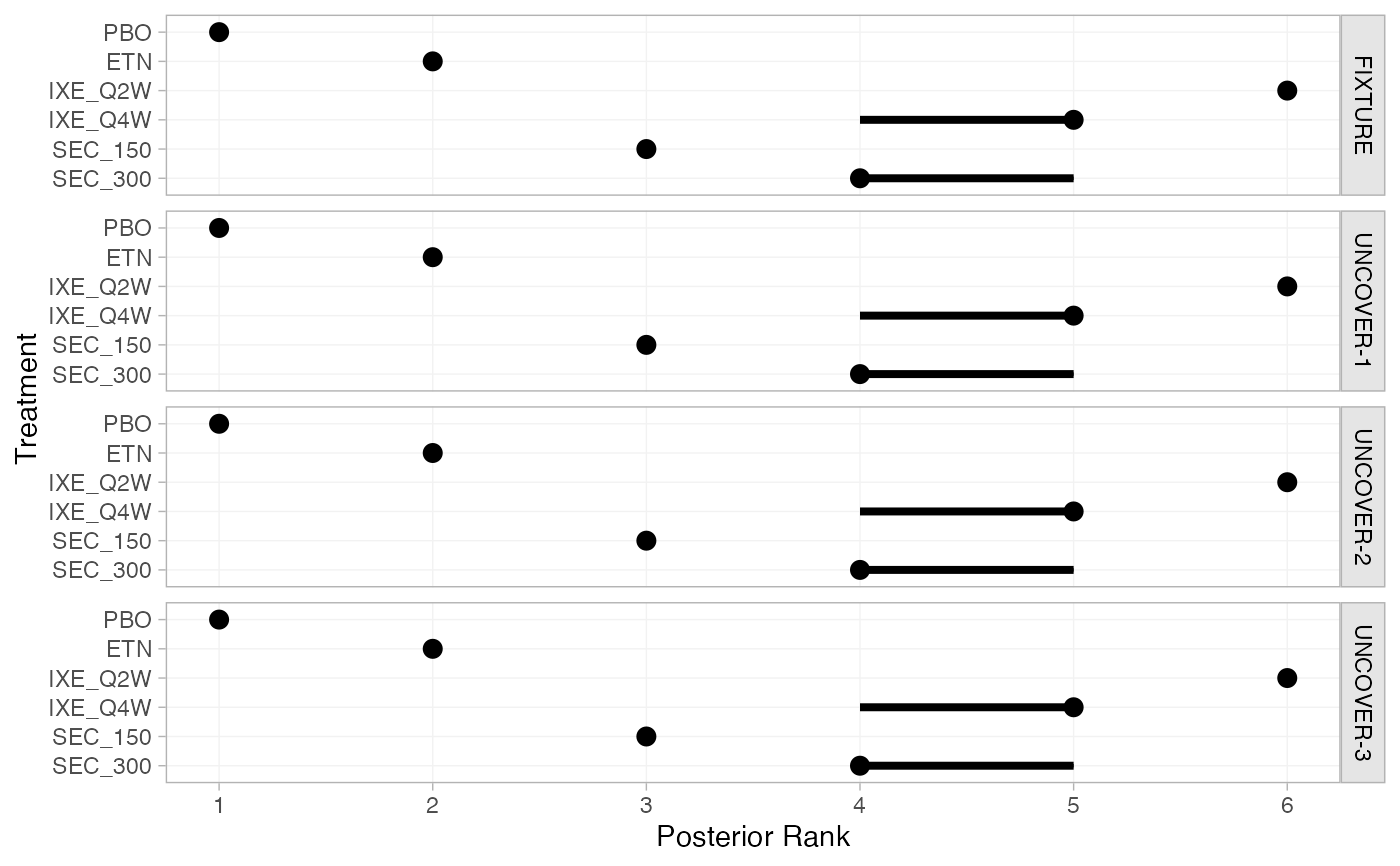 # Rank probabilities
pso_rankprobs <- posterior_rank_probs(pso_fit)
pso_rankprobs
#> ---------------------------------------------------------------- Study: FIXTURE ----
#>
#> Covariate values:
#> durnpso prevsys bsa weight psa
#> 1.6 0.62 0.34 8.34 0.14
#>
#> p_rank[1] p_rank[2] p_rank[3] p_rank[4] p_rank[5] p_rank[6]
#> d[FIXTURE: PBO] 1 0 0 0.00 0.00 0
#> d[FIXTURE: ETN] 0 1 0 0.00 0.00 0
#> d[FIXTURE: IXE_Q2W] 0 0 0 0.00 0.00 1
#> d[FIXTURE: IXE_Q4W] 0 0 0 0.22 0.78 0
#> d[FIXTURE: SEC_150] 0 0 1 0.00 0.00 0
#> d[FIXTURE: SEC_300] 0 0 0 0.78 0.22 0
#>
#> -------------------------------------------------------------- Study: UNCOVER-1 ----
#>
#> Covariate values:
#> durnpso prevsys bsa weight psa
#> 2 0.73 0.28 9.24 0.28
#>
#> p_rank[1] p_rank[2] p_rank[3] p_rank[4] p_rank[5]
#> d[UNCOVER-1: PBO] 1 0 0 0.00 0.00
#> d[UNCOVER-1: ETN] 0 1 0 0.00 0.00
#> d[UNCOVER-1: IXE_Q2W] 0 0 0 0.00 0.00
#> d[UNCOVER-1: IXE_Q4W] 0 0 0 0.22 0.78
#> d[UNCOVER-1: SEC_150] 0 0 1 0.00 0.00
#> d[UNCOVER-1: SEC_300] 0 0 0 0.78 0.22
#> p_rank[6]
#> d[UNCOVER-1: PBO] 0
#> d[UNCOVER-1: ETN] 0
#> d[UNCOVER-1: IXE_Q2W] 1
#> d[UNCOVER-1: IXE_Q4W] 0
#> d[UNCOVER-1: SEC_150] 0
#> d[UNCOVER-1: SEC_300] 0
#>
#> -------------------------------------------------------------- Study: UNCOVER-2 ----
#>
#> Covariate values:
#> durnpso prevsys bsa weight psa
#> 1.87 0.64 0.27 9.17 0.24
#>
#> p_rank[1] p_rank[2] p_rank[3] p_rank[4] p_rank[5]
#> d[UNCOVER-2: PBO] 1 0 0 0.00 0.00
#> d[UNCOVER-2: ETN] 0 1 0 0.00 0.00
#> d[UNCOVER-2: IXE_Q2W] 0 0 0 0.00 0.00
#> d[UNCOVER-2: IXE_Q4W] 0 0 0 0.22 0.78
#> d[UNCOVER-2: SEC_150] 0 0 1 0.00 0.00
#> d[UNCOVER-2: SEC_300] 0 0 0 0.78 0.22
#> p_rank[6]
#> d[UNCOVER-2: PBO] 0
#> d[UNCOVER-2: ETN] 0
#> d[UNCOVER-2: IXE_Q2W] 1
#> d[UNCOVER-2: IXE_Q4W] 0
#> d[UNCOVER-2: SEC_150] 0
#> d[UNCOVER-2: SEC_300] 0
#>
#> -------------------------------------------------------------- Study: UNCOVER-3 ----
#>
#> Covariate values:
#> durnpso prevsys bsa weight psa
#> 1.78 0.59 0.28 9.01 0.2
#>
#> p_rank[1] p_rank[2] p_rank[3] p_rank[4] p_rank[5]
#> d[UNCOVER-3: PBO] 1 0 0 0.00 0.00
#> d[UNCOVER-3: ETN] 0 1 0 0.00 0.00
#> d[UNCOVER-3: IXE_Q2W] 0 0 0 0.00 0.00
#> d[UNCOVER-3: IXE_Q4W] 0 0 0 0.22 0.78
#> d[UNCOVER-3: SEC_150] 0 0 1 0.00 0.00
#> d[UNCOVER-3: SEC_300] 0 0 0 0.78 0.22
#> p_rank[6]
#> d[UNCOVER-3: PBO] 0
#> d[UNCOVER-3: ETN] 0
#> d[UNCOVER-3: IXE_Q2W] 1
#> d[UNCOVER-3: IXE_Q4W] 0
#> d[UNCOVER-3: SEC_150] 0
#> d[UNCOVER-3: SEC_300] 0
#>
plot(pso_rankprobs)
# Rank probabilities
pso_rankprobs <- posterior_rank_probs(pso_fit)
pso_rankprobs
#> ---------------------------------------------------------------- Study: FIXTURE ----
#>
#> Covariate values:
#> durnpso prevsys bsa weight psa
#> 1.6 0.62 0.34 8.34 0.14
#>
#> p_rank[1] p_rank[2] p_rank[3] p_rank[4] p_rank[5] p_rank[6]
#> d[FIXTURE: PBO] 1 0 0 0.00 0.00 0
#> d[FIXTURE: ETN] 0 1 0 0.00 0.00 0
#> d[FIXTURE: IXE_Q2W] 0 0 0 0.00 0.00 1
#> d[FIXTURE: IXE_Q4W] 0 0 0 0.22 0.78 0
#> d[FIXTURE: SEC_150] 0 0 1 0.00 0.00 0
#> d[FIXTURE: SEC_300] 0 0 0 0.78 0.22 0
#>
#> -------------------------------------------------------------- Study: UNCOVER-1 ----
#>
#> Covariate values:
#> durnpso prevsys bsa weight psa
#> 2 0.73 0.28 9.24 0.28
#>
#> p_rank[1] p_rank[2] p_rank[3] p_rank[4] p_rank[5]
#> d[UNCOVER-1: PBO] 1 0 0 0.00 0.00
#> d[UNCOVER-1: ETN] 0 1 0 0.00 0.00
#> d[UNCOVER-1: IXE_Q2W] 0 0 0 0.00 0.00
#> d[UNCOVER-1: IXE_Q4W] 0 0 0 0.22 0.78
#> d[UNCOVER-1: SEC_150] 0 0 1 0.00 0.00
#> d[UNCOVER-1: SEC_300] 0 0 0 0.78 0.22
#> p_rank[6]
#> d[UNCOVER-1: PBO] 0
#> d[UNCOVER-1: ETN] 0
#> d[UNCOVER-1: IXE_Q2W] 1
#> d[UNCOVER-1: IXE_Q4W] 0
#> d[UNCOVER-1: SEC_150] 0
#> d[UNCOVER-1: SEC_300] 0
#>
#> -------------------------------------------------------------- Study: UNCOVER-2 ----
#>
#> Covariate values:
#> durnpso prevsys bsa weight psa
#> 1.87 0.64 0.27 9.17 0.24
#>
#> p_rank[1] p_rank[2] p_rank[3] p_rank[4] p_rank[5]
#> d[UNCOVER-2: PBO] 1 0 0 0.00 0.00
#> d[UNCOVER-2: ETN] 0 1 0 0.00 0.00
#> d[UNCOVER-2: IXE_Q2W] 0 0 0 0.00 0.00
#> d[UNCOVER-2: IXE_Q4W] 0 0 0 0.22 0.78
#> d[UNCOVER-2: SEC_150] 0 0 1 0.00 0.00
#> d[UNCOVER-2: SEC_300] 0 0 0 0.78 0.22
#> p_rank[6]
#> d[UNCOVER-2: PBO] 0
#> d[UNCOVER-2: ETN] 0
#> d[UNCOVER-2: IXE_Q2W] 1
#> d[UNCOVER-2: IXE_Q4W] 0
#> d[UNCOVER-2: SEC_150] 0
#> d[UNCOVER-2: SEC_300] 0
#>
#> -------------------------------------------------------------- Study: UNCOVER-3 ----
#>
#> Covariate values:
#> durnpso prevsys bsa weight psa
#> 1.78 0.59 0.28 9.01 0.2
#>
#> p_rank[1] p_rank[2] p_rank[3] p_rank[4] p_rank[5]
#> d[UNCOVER-3: PBO] 1 0 0 0.00 0.00
#> d[UNCOVER-3: ETN] 0 1 0 0.00 0.00
#> d[UNCOVER-3: IXE_Q2W] 0 0 0 0.00 0.00
#> d[UNCOVER-3: IXE_Q4W] 0 0 0 0.22 0.78
#> d[UNCOVER-3: SEC_150] 0 0 1 0.00 0.00
#> d[UNCOVER-3: SEC_300] 0 0 0 0.78 0.22
#> p_rank[6]
#> d[UNCOVER-3: PBO] 0
#> d[UNCOVER-3: ETN] 0
#> d[UNCOVER-3: IXE_Q2W] 1
#> d[UNCOVER-3: IXE_Q4W] 0
#> d[UNCOVER-3: SEC_150] 0
#> d[UNCOVER-3: SEC_300] 0
#>
plot(pso_rankprobs)
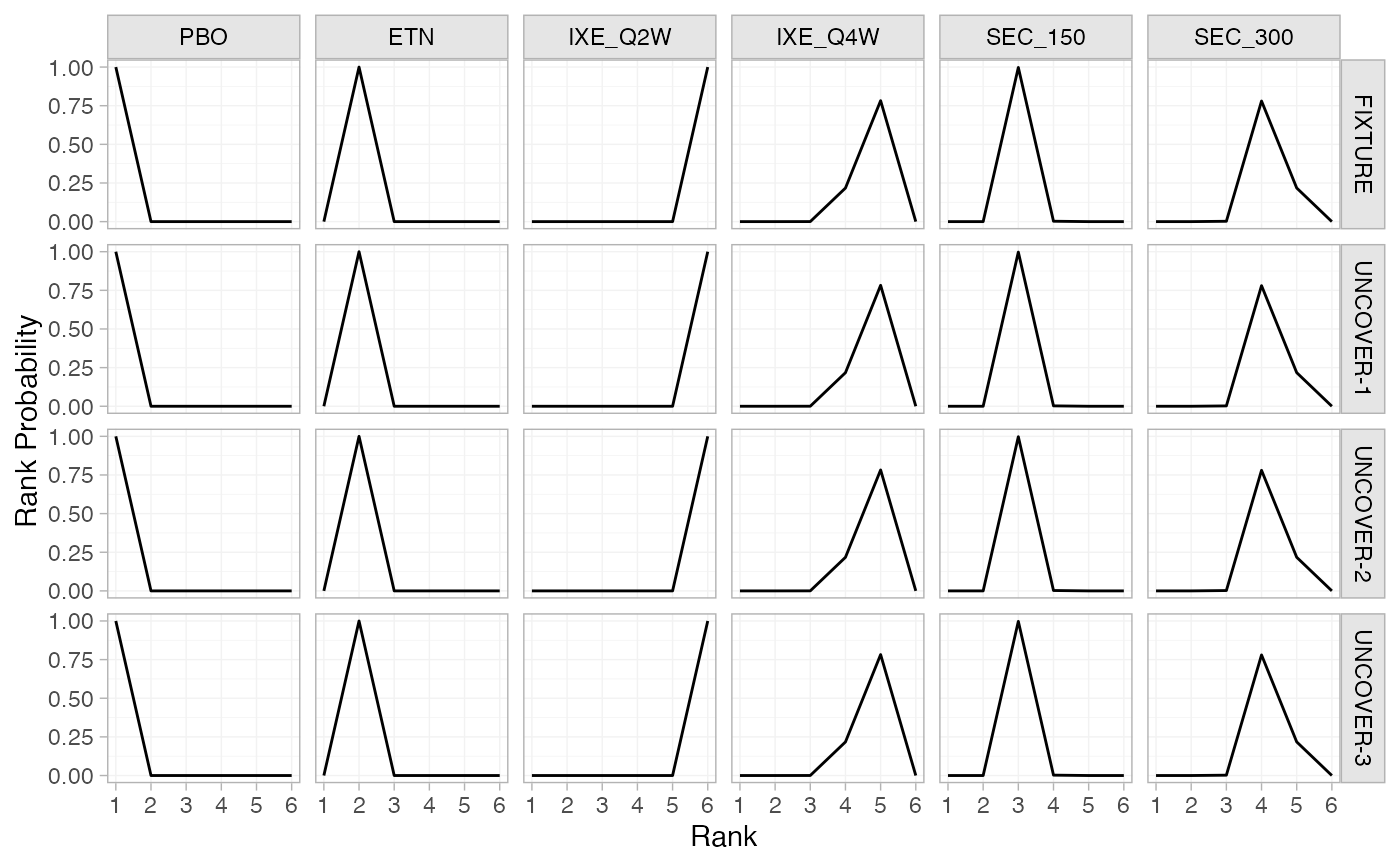 # Cumulative rank probabilities
pso_cumrankprobs <- posterior_rank_probs(pso_fit, cumulative = TRUE)
pso_cumrankprobs
#> ---------------------------------------------------------------- Study: FIXTURE ----
#>
#> Covariate values:
#> durnpso prevsys bsa weight psa
#> 1.6 0.62 0.34 8.34 0.14
#>
#> p_rank[1] p_rank[2] p_rank[3] p_rank[4] p_rank[5] p_rank[6]
#> d[FIXTURE: PBO] 1 1 1 1.00 1 1
#> d[FIXTURE: ETN] 0 1 1 1.00 1 1
#> d[FIXTURE: IXE_Q2W] 0 0 0 0.00 0 1
#> d[FIXTURE: IXE_Q4W] 0 0 0 0.22 1 1
#> d[FIXTURE: SEC_150] 0 0 1 1.00 1 1
#> d[FIXTURE: SEC_300] 0 0 0 0.78 1 1
#>
#> -------------------------------------------------------------- Study: UNCOVER-1 ----
#>
#> Covariate values:
#> durnpso prevsys bsa weight psa
#> 2 0.73 0.28 9.24 0.28
#>
#> p_rank[1] p_rank[2] p_rank[3] p_rank[4] p_rank[5]
#> d[UNCOVER-1: PBO] 1 1 1 1.00 1
#> d[UNCOVER-1: ETN] 0 1 1 1.00 1
#> d[UNCOVER-1: IXE_Q2W] 0 0 0 0.00 0
#> d[UNCOVER-1: IXE_Q4W] 0 0 0 0.22 1
#> d[UNCOVER-1: SEC_150] 0 0 1 1.00 1
#> d[UNCOVER-1: SEC_300] 0 0 0 0.78 1
#> p_rank[6]
#> d[UNCOVER-1: PBO] 1
#> d[UNCOVER-1: ETN] 1
#> d[UNCOVER-1: IXE_Q2W] 1
#> d[UNCOVER-1: IXE_Q4W] 1
#> d[UNCOVER-1: SEC_150] 1
#> d[UNCOVER-1: SEC_300] 1
#>
#> -------------------------------------------------------------- Study: UNCOVER-2 ----
#>
#> Covariate values:
#> durnpso prevsys bsa weight psa
#> 1.87 0.64 0.27 9.17 0.24
#>
#> p_rank[1] p_rank[2] p_rank[3] p_rank[4] p_rank[5]
#> d[UNCOVER-2: PBO] 1 1 1 1.00 1
#> d[UNCOVER-2: ETN] 0 1 1 1.00 1
#> d[UNCOVER-2: IXE_Q2W] 0 0 0 0.00 0
#> d[UNCOVER-2: IXE_Q4W] 0 0 0 0.22 1
#> d[UNCOVER-2: SEC_150] 0 0 1 1.00 1
#> d[UNCOVER-2: SEC_300] 0 0 0 0.78 1
#> p_rank[6]
#> d[UNCOVER-2: PBO] 1
#> d[UNCOVER-2: ETN] 1
#> d[UNCOVER-2: IXE_Q2W] 1
#> d[UNCOVER-2: IXE_Q4W] 1
#> d[UNCOVER-2: SEC_150] 1
#> d[UNCOVER-2: SEC_300] 1
#>
#> -------------------------------------------------------------- Study: UNCOVER-3 ----
#>
#> Covariate values:
#> durnpso prevsys bsa weight psa
#> 1.78 0.59 0.28 9.01 0.2
#>
#> p_rank[1] p_rank[2] p_rank[3] p_rank[4] p_rank[5]
#> d[UNCOVER-3: PBO] 1 1 1 1.00 1
#> d[UNCOVER-3: ETN] 0 1 1 1.00 1
#> d[UNCOVER-3: IXE_Q2W] 0 0 0 0.00 0
#> d[UNCOVER-3: IXE_Q4W] 0 0 0 0.22 1
#> d[UNCOVER-3: SEC_150] 0 0 1 1.00 1
#> d[UNCOVER-3: SEC_300] 0 0 0 0.78 1
#> p_rank[6]
#> d[UNCOVER-3: PBO] 1
#> d[UNCOVER-3: ETN] 1
#> d[UNCOVER-3: IXE_Q2W] 1
#> d[UNCOVER-3: IXE_Q4W] 1
#> d[UNCOVER-3: SEC_150] 1
#> d[UNCOVER-3: SEC_300] 1
#>
plot(pso_cumrankprobs)
# Cumulative rank probabilities
pso_cumrankprobs <- posterior_rank_probs(pso_fit, cumulative = TRUE)
pso_cumrankprobs
#> ---------------------------------------------------------------- Study: FIXTURE ----
#>
#> Covariate values:
#> durnpso prevsys bsa weight psa
#> 1.6 0.62 0.34 8.34 0.14
#>
#> p_rank[1] p_rank[2] p_rank[3] p_rank[4] p_rank[5] p_rank[6]
#> d[FIXTURE: PBO] 1 1 1 1.00 1 1
#> d[FIXTURE: ETN] 0 1 1 1.00 1 1
#> d[FIXTURE: IXE_Q2W] 0 0 0 0.00 0 1
#> d[FIXTURE: IXE_Q4W] 0 0 0 0.22 1 1
#> d[FIXTURE: SEC_150] 0 0 1 1.00 1 1
#> d[FIXTURE: SEC_300] 0 0 0 0.78 1 1
#>
#> -------------------------------------------------------------- Study: UNCOVER-1 ----
#>
#> Covariate values:
#> durnpso prevsys bsa weight psa
#> 2 0.73 0.28 9.24 0.28
#>
#> p_rank[1] p_rank[2] p_rank[3] p_rank[4] p_rank[5]
#> d[UNCOVER-1: PBO] 1 1 1 1.00 1
#> d[UNCOVER-1: ETN] 0 1 1 1.00 1
#> d[UNCOVER-1: IXE_Q2W] 0 0 0 0.00 0
#> d[UNCOVER-1: IXE_Q4W] 0 0 0 0.22 1
#> d[UNCOVER-1: SEC_150] 0 0 1 1.00 1
#> d[UNCOVER-1: SEC_300] 0 0 0 0.78 1
#> p_rank[6]
#> d[UNCOVER-1: PBO] 1
#> d[UNCOVER-1: ETN] 1
#> d[UNCOVER-1: IXE_Q2W] 1
#> d[UNCOVER-1: IXE_Q4W] 1
#> d[UNCOVER-1: SEC_150] 1
#> d[UNCOVER-1: SEC_300] 1
#>
#> -------------------------------------------------------------- Study: UNCOVER-2 ----
#>
#> Covariate values:
#> durnpso prevsys bsa weight psa
#> 1.87 0.64 0.27 9.17 0.24
#>
#> p_rank[1] p_rank[2] p_rank[3] p_rank[4] p_rank[5]
#> d[UNCOVER-2: PBO] 1 1 1 1.00 1
#> d[UNCOVER-2: ETN] 0 1 1 1.00 1
#> d[UNCOVER-2: IXE_Q2W] 0 0 0 0.00 0
#> d[UNCOVER-2: IXE_Q4W] 0 0 0 0.22 1
#> d[UNCOVER-2: SEC_150] 0 0 1 1.00 1
#> d[UNCOVER-2: SEC_300] 0 0 0 0.78 1
#> p_rank[6]
#> d[UNCOVER-2: PBO] 1
#> d[UNCOVER-2: ETN] 1
#> d[UNCOVER-2: IXE_Q2W] 1
#> d[UNCOVER-2: IXE_Q4W] 1
#> d[UNCOVER-2: SEC_150] 1
#> d[UNCOVER-2: SEC_300] 1
#>
#> -------------------------------------------------------------- Study: UNCOVER-3 ----
#>
#> Covariate values:
#> durnpso prevsys bsa weight psa
#> 1.78 0.59 0.28 9.01 0.2
#>
#> p_rank[1] p_rank[2] p_rank[3] p_rank[4] p_rank[5]
#> d[UNCOVER-3: PBO] 1 1 1 1.00 1
#> d[UNCOVER-3: ETN] 0 1 1 1.00 1
#> d[UNCOVER-3: IXE_Q2W] 0 0 0 0.00 0
#> d[UNCOVER-3: IXE_Q4W] 0 0 0 0.22 1
#> d[UNCOVER-3: SEC_150] 0 0 1 1.00 1
#> d[UNCOVER-3: SEC_300] 0 0 0 0.78 1
#> p_rank[6]
#> d[UNCOVER-3: PBO] 1
#> d[UNCOVER-3: ETN] 1
#> d[UNCOVER-3: IXE_Q2W] 1
#> d[UNCOVER-3: IXE_Q4W] 1
#> d[UNCOVER-3: SEC_150] 1
#> d[UNCOVER-3: SEC_300] 1
#>
plot(pso_cumrankprobs)
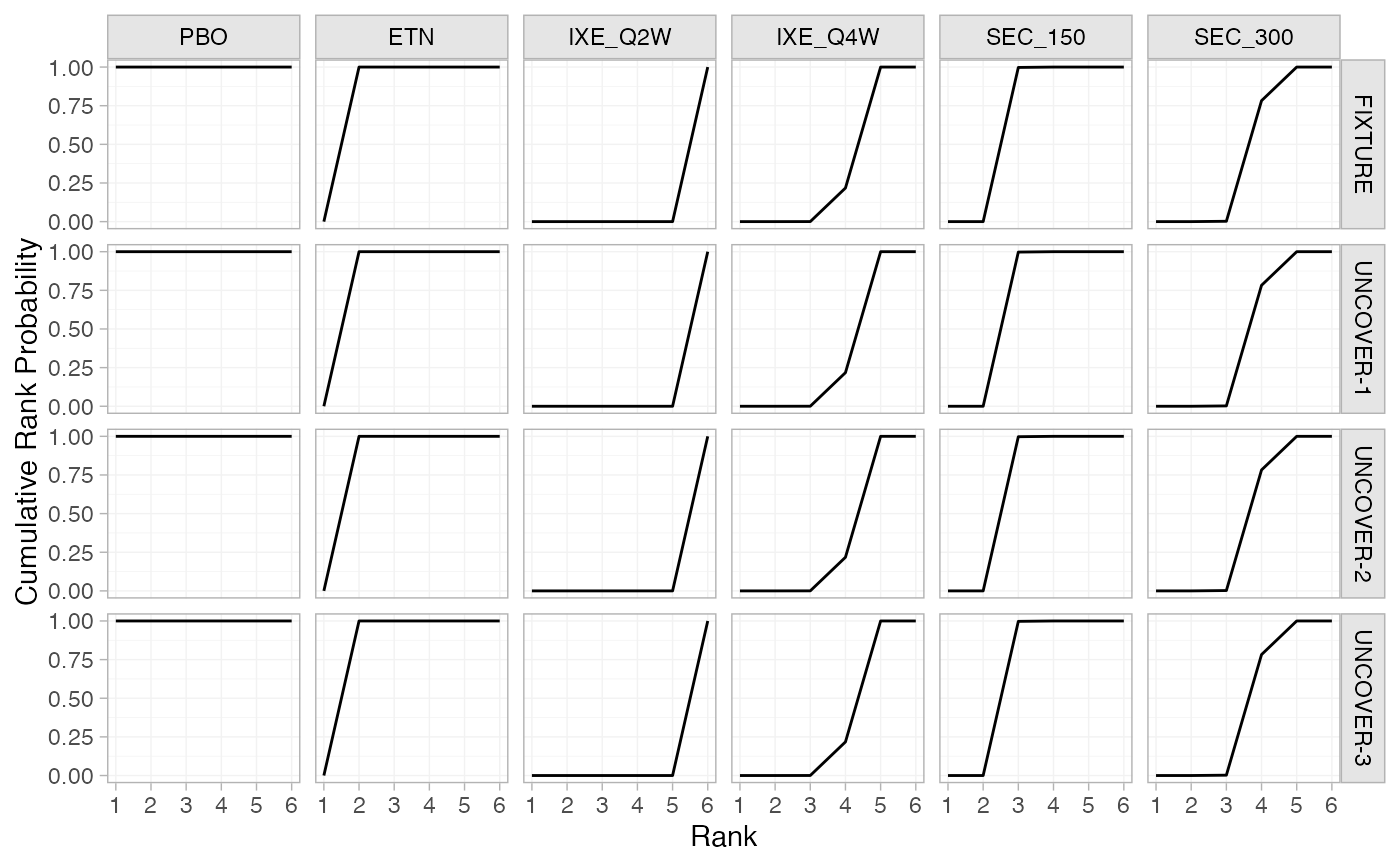 # Produce population-adjusted rankings for a different target
# population
new_agd_means <- data.frame(
bsa = 0.6,
prevsys = 0.1,
psa = 0.2,
weight = 10,
durnpso = 3)
# Ranks
posterior_ranks(pso_fit, newdata = new_agd_means)
#> ------------------------------------------------------------------ Study: New 1 ----
#>
#> Covariate values:
#> durnpso prevsys bsa weight psa
#> 3 0.1 0.6 10 0.2
#>
#> mean sd 2.5% 25% 50% 75% 97.5% Bulk_ESS Tail_ESS Rhat
#> rank[New 1: PBO] 1.00 0.00 1 1 1 1 1 NA NA NA
#> rank[New 1: ETN] 2.00 0.00 2 2 2 2 2 NA NA NA
#> rank[New 1: IXE_Q2W] 6.00 0.00 6 6 6 6 6 NA NA NA
#> rank[New 1: IXE_Q4W] 4.78 0.41 4 5 5 5 5 4047 NA 1
#> rank[New 1: SEC_150] 3.00 0.05 3 3 3 3 3 3397 3397 1
#> rank[New 1: SEC_300] 4.22 0.42 4 4 4 4 5 4130 NA 1
#>
# Rank probabilities
posterior_rank_probs(pso_fit, newdata = new_agd_means)
#> ------------------------------------------------------------------ Study: New 1 ----
#>
#> Covariate values:
#> durnpso prevsys bsa weight psa
#> 3 0.1 0.6 10 0.2
#>
#> p_rank[1] p_rank[2] p_rank[3] p_rank[4] p_rank[5] p_rank[6]
#> d[New 1: PBO] 1 0 0 0.00 0.00 0
#> d[New 1: ETN] 0 1 0 0.00 0.00 0
#> d[New 1: IXE_Q2W] 0 0 0 0.00 0.00 1
#> d[New 1: IXE_Q4W] 0 0 0 0.22 0.78 0
#> d[New 1: SEC_150] 0 0 1 0.00 0.00 0
#> d[New 1: SEC_300] 0 0 0 0.78 0.22 0
#>
# Cumulative rank probabilities
posterior_rank_probs(pso_fit, newdata = new_agd_means,
cumulative = TRUE)
#> ------------------------------------------------------------------ Study: New 1 ----
#>
#> Covariate values:
#> durnpso prevsys bsa weight psa
#> 3 0.1 0.6 10 0.2
#>
#> p_rank[1] p_rank[2] p_rank[3] p_rank[4] p_rank[5] p_rank[6]
#> d[New 1: PBO] 1 1 1 1.00 1 1
#> d[New 1: ETN] 0 1 1 1.00 1 1
#> d[New 1: IXE_Q2W] 0 0 0 0.00 0 1
#> d[New 1: IXE_Q4W] 0 0 0 0.22 1 1
#> d[New 1: SEC_150] 0 0 1 1.00 1 1
#> d[New 1: SEC_300] 0 0 0 0.78 1 1
#>
# }
# Produce population-adjusted rankings for a different target
# population
new_agd_means <- data.frame(
bsa = 0.6,
prevsys = 0.1,
psa = 0.2,
weight = 10,
durnpso = 3)
# Ranks
posterior_ranks(pso_fit, newdata = new_agd_means)
#> ------------------------------------------------------------------ Study: New 1 ----
#>
#> Covariate values:
#> durnpso prevsys bsa weight psa
#> 3 0.1 0.6 10 0.2
#>
#> mean sd 2.5% 25% 50% 75% 97.5% Bulk_ESS Tail_ESS Rhat
#> rank[New 1: PBO] 1.00 0.00 1 1 1 1 1 NA NA NA
#> rank[New 1: ETN] 2.00 0.00 2 2 2 2 2 NA NA NA
#> rank[New 1: IXE_Q2W] 6.00 0.00 6 6 6 6 6 NA NA NA
#> rank[New 1: IXE_Q4W] 4.78 0.41 4 5 5 5 5 4047 NA 1
#> rank[New 1: SEC_150] 3.00 0.05 3 3 3 3 3 3397 3397 1
#> rank[New 1: SEC_300] 4.22 0.42 4 4 4 4 5 4130 NA 1
#>
# Rank probabilities
posterior_rank_probs(pso_fit, newdata = new_agd_means)
#> ------------------------------------------------------------------ Study: New 1 ----
#>
#> Covariate values:
#> durnpso prevsys bsa weight psa
#> 3 0.1 0.6 10 0.2
#>
#> p_rank[1] p_rank[2] p_rank[3] p_rank[4] p_rank[5] p_rank[6]
#> d[New 1: PBO] 1 0 0 0.00 0.00 0
#> d[New 1: ETN] 0 1 0 0.00 0.00 0
#> d[New 1: IXE_Q2W] 0 0 0 0.00 0.00 1
#> d[New 1: IXE_Q4W] 0 0 0 0.22 0.78 0
#> d[New 1: SEC_150] 0 0 1 0.00 0.00 0
#> d[New 1: SEC_300] 0 0 0 0.78 0.22 0
#>
# Cumulative rank probabilities
posterior_rank_probs(pso_fit, newdata = new_agd_means,
cumulative = TRUE)
#> ------------------------------------------------------------------ Study: New 1 ----
#>
#> Covariate values:
#> durnpso prevsys bsa weight psa
#> 3 0.1 0.6 10 0.2
#>
#> p_rank[1] p_rank[2] p_rank[3] p_rank[4] p_rank[5] p_rank[6]
#> d[New 1: PBO] 1 1 1 1.00 1 1
#> d[New 1: ETN] 0 1 1 1.00 1 1
#> d[New 1: IXE_Q2W] 0 0 0 0.00 0 1
#> d[New 1: IXE_Q4W] 0 0 0 0.22 1 1
#> d[New 1: SEC_150] 0 0 1 1.00 1 1
#> d[New 1: SEC_300] 0 0 0 0.78 1 1
#>
# }